- 控制之美.卷1,控制理论从传递函数到状态空间/王天威编著.-北京:清华大学出版社,2022. 7 ISBN 978-7-302-60975-9
- 工程控制论
- 自动控制原理
元件/算子/变换/系统 的性质
函数是输入数值输出数值
泛函是输入序列(函数)输出数值
而这里是输入序列(函数)输出序列(函数)
在电路原理叫 元件
在人工智能叫 算子
在复变函数叫 变换
在自动控制叫 系统
因果性
输出,只与当前信息和以前的信息有关。
对于数字图像处理,显然可以没有因果性。
无记忆性
算子被贬为函数了
可以粗浅地理解为表达式只含有对u的代数运算,不含u的导数、u的积分等运算。
此时
线性
这不是函数的线性,而是变换的线性!
也就是说,
时不变性(定常性)
输入时间延迟,输出时间也延迟,波形不变。
比方说,时钟并不会随着时间流逝而加快。(如果有,应该是谁拨快了时钟——随时间变化的参数介入,但又不像输入一样受到延迟——或许孤立系统都是时不变系统)
内稳性、渐进性、有界性、吸引性
李雅普诺夫稳定性与经典稳定性 - 知乎
李雅普诺夫稳定性理论(万字长文,全网最全!) - 知乎
控制理论中关于连续,稳定,有界等几个概念的区别与联系? - 知乎
现代控制理论中的吸引、一致吸引、全局吸引、全局一致吸引怎么生动理解? - 知乎
非线性系统(Nonlinear Systems)—4.7 有界性、最终有界性和输入-状态稳定性(ISS) - 知乎
稳定&渐进稳定,一致有界&一致最终有界-CSDN博客
现代控制理论学习笔记 - 第五章:系统稳定性
渐进稳定性与有界输入有界输出稳定性 - 哔哩哔哩
如何理解李雅普诺夫稳定性分析 - 知乎
人话:考虑一个无输入(瞬时扰动消失并留下初态偏差)的状态空间方程表达式,经过足够长的时间,
- 若存在初态界限,
可以未来具有界限,系统终究不会跑远,则系统是李雅普诺夫意义下的稳定的。若 不依赖于 则一致稳定。 - 若存在初态界限,
可以 未来趋近于零,系统终究能回到原来的平衡状态,则系统是渐进稳定的。若 不依赖于 则一致渐进稳定。 - 若放开初态条件,
都可以 未来具有界限,则系统是一致有界(全局稳定)的。 - 若放开初态条件,
都可以 未来趋近于零,则系统是一致吸引(全局渐进稳定)的。 - 若不属于这样的情况,
趋近于发散,回不到平衡了,则系统是不稳定的。
数学话:李雅普诺夫意义下的稳定性——给定
数学话:渐进稳定性
在这种情况下,称系统的平衡点
如果
若放开
经典控制理论中,稳定专指渐进稳定,李雅普诺夫意义下稳定称为临界稳定或不稳定。
外稳性
控制理论中的几种稳定性介绍_uniformly ultimately bounded-CSDN博客
系统的输入到状态稳定性 | 辛未羊的网络日志
李雅普诺夫稳定(内部稳定)与BIBO稳定(外部稳定)的关系_bibo稳定与内部稳定-CSDN博客
李雅普诺夫稳定,输入输出稳定,输入状态稳定三者有什么区别? - 知乎
稳定性分析+李氏稳定+BIBS(全)稳定+BIBO(全)稳定+全局稳定 - 哔哩哔哩
现代控制理论学习笔记 - 第五章:系统稳定性
有界输入有界输出稳定性-数学百科
信号与系统:BIBO稳定性判据 - 技术教程
(8 封私信) 非线性系统(Nonlinear Systems)—4.7 有界性、最终有界性和输入-状态稳定性(ISS) - 知乎
非线性系统(Nonlinear Systems)—5 输入-输出稳定性(Input-to-Output Stability) - 知乎
人话
- 系统的任意有界输入都产生的是有界状态,则系统有BIBS稳定性(有界输入有界状态稳定性)
- 系统的任意有界输入都产生的是有界输出,则系统有BIBO稳定性(有界输入有界输出稳定性)
数学话:输入状态稳定性

在有输入的情况下,
外稳不一定内稳,因为内部不稳定的子状态可能是不能观的,内部的不稳定不会体现在外界观测。
内稳则一定外稳。
无输入情况下,针对完全能控能观的线性系统,输入输出稳定、输入状态稳定、李雅普诺夫稳定,等价。
渐进稳定下,满足输入输出稳定。因可根据定义,得到冲激响应的积分(单位阶跃响应)有界。
临界稳定(非渐进稳定)下,不满足输入输出稳定。可以用有限的输入对系统造成共振。
能控性、能观性
线性系统理论(三)能控性与能观性 - 知乎
存在输入
能在有限时间区间内
将系统的状态变量从
一个时间连续的线性系统:
在有限的时间间隔内
已知系统的输入量
测得系统的输出量
可以唯一确定系统的初始状态
那么就称这个时连系统是 完全可观(vollständig beobachtbar)的。
系统的表示
非线性系统分析,描述函数法中的等效线性环节、等效非线性环节,怎么求? - 知乎
如何理解李雅普诺夫稳定性分析 - 知乎
线性时不变微分方程→传递函数
为什么传递函数只能描述线性定常系统而不适合时变系统? - 知乎
我们只针对线性时不变系统用传递函数来表示(非线性系统可以使用描述函数)
定义:零初始条件下,输出拉氏变换和输入拉氏变换的比。
对于两个序列的关系,自然想到用微分方程表示。
我们对微分方程进行算子法表示,即拉普拉斯变换。
把输出拉氏变换除以输入拉氏变换,可以得到一个比值称为传递函数
有什么意义呢?根据拉普拉斯变换的卷积性质
正好就是从冲激响应的角度对元件的理解。
对于线性系统:标准形式/有理分式形式/多项式形式
对于线性系统时域分析法:时间常数形式/典型环节形式/尾1形式。提取尾部系数
对于线性系统根轨迹法:零极点增益形式/根的形式/首1形式。提取首部系数
对于特征多项式
传递函数的分母
由于现实中输出的阶次鲜有比输入的阶次高,特征多项式的阶次即称为系统的阶次
对于初始状态非零
初始输入非零,根据时不变性,可以视为初始输入为零,而经过瞬时阶跃变成非零
初始输出非零,则以一阶系统为例,
六大典型环节(传递函数宜记忆)——比例、积分、微分、惯性、振荡、时滞
对于逆系统,即两个系统串联,传递函数互为相反数。
传递函数的图表示
特征多项式的唯一性
如果扰动量从上面进入(如图),则分母不变,分子加入
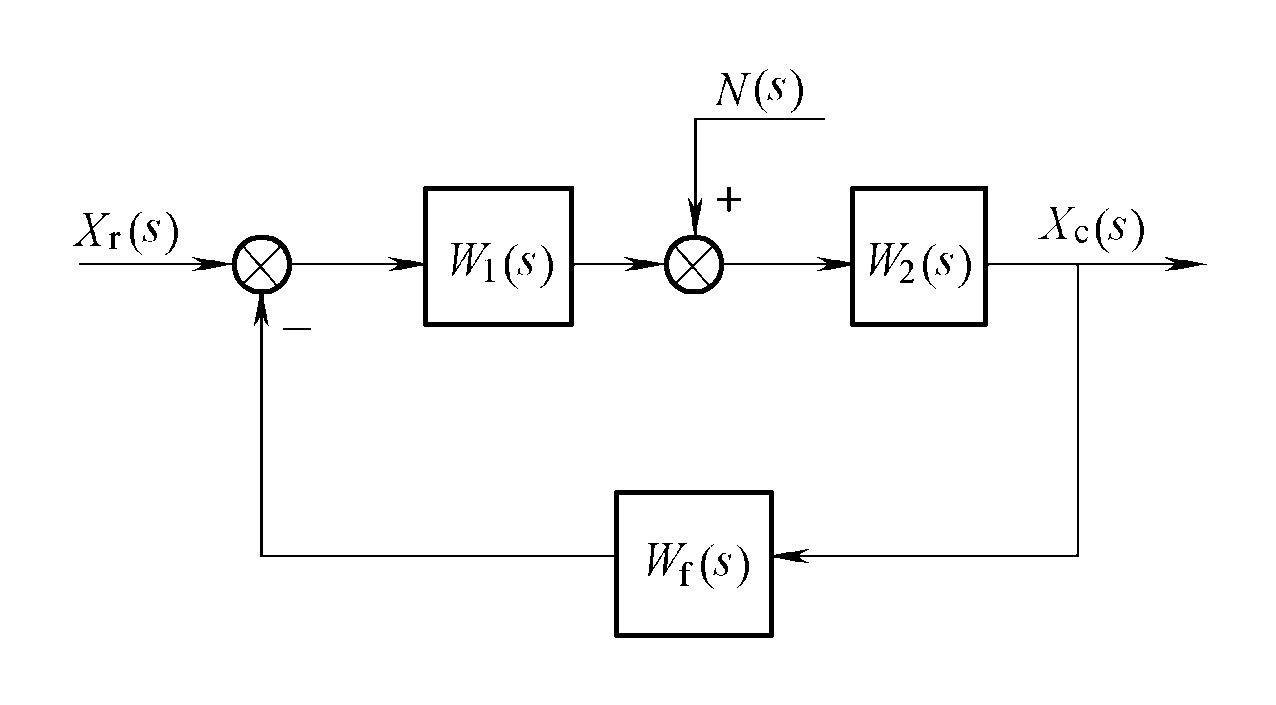
如果扰动量从下面进入,还是分母不变,分子加入
所以,分母不会变。
对于反馈连接:根轨迹法、奈奎斯特辅助函数法
定义开环传递函数
注意,开环传递函数相当于切断最外层反馈,引入测试输入和测试输出,求测试环节的传递函数。
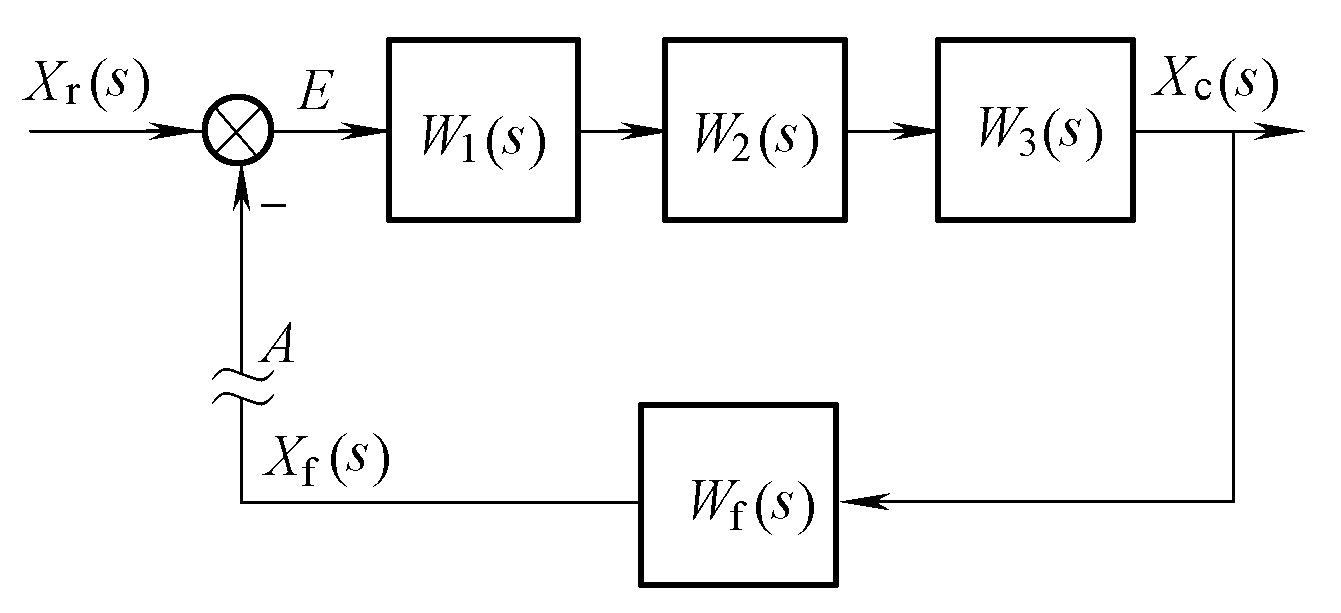
所以,下图的开环传递函数很容易搞错,不要把变位后的信号线也接入测试端!
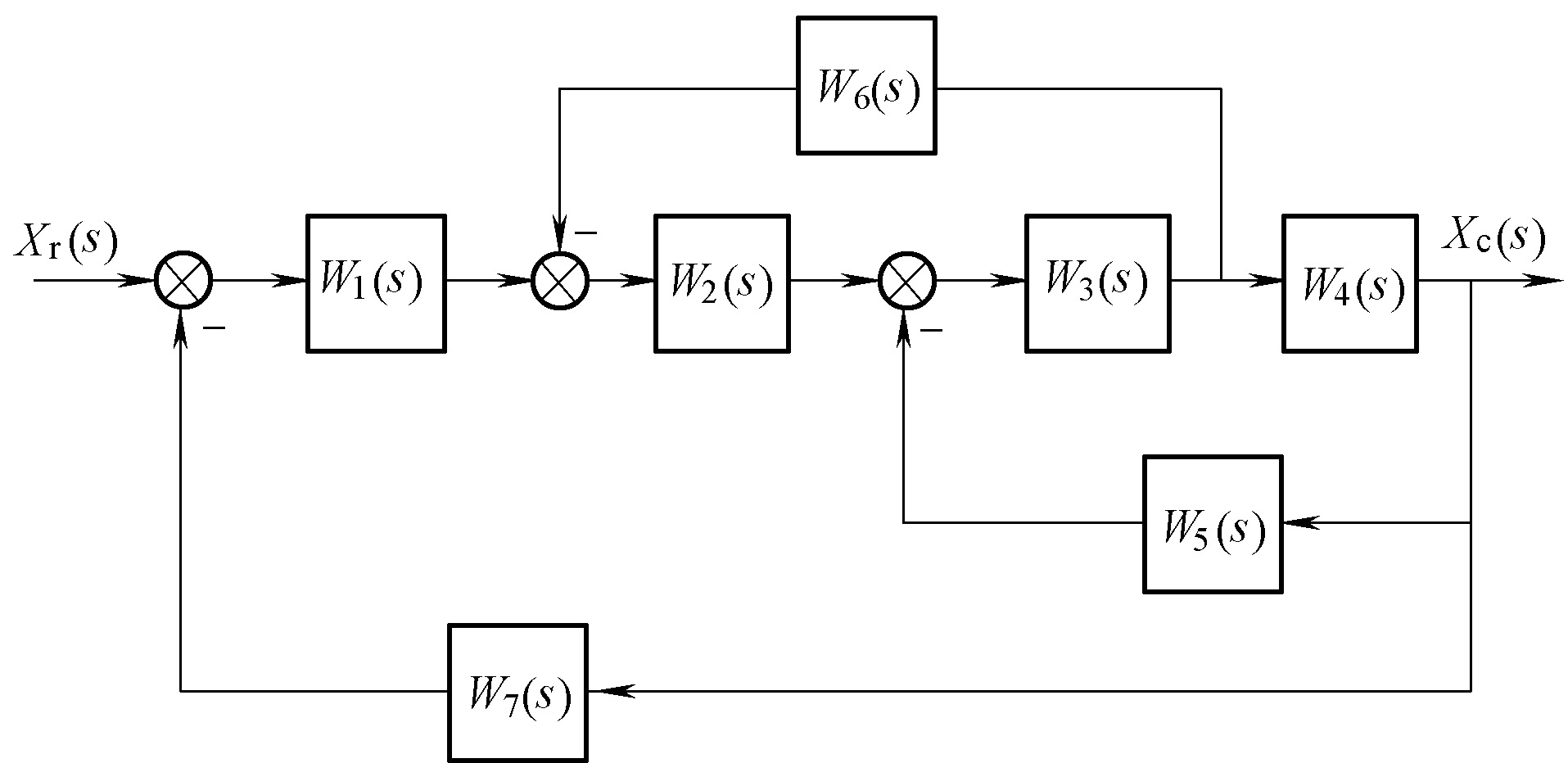
对于负反馈连接的等效传递函数
咋给我来个调和平均数?这是巧合还是可以联系到电路并联?我想到了运放的加法电路。梅逊增益公式的前身?
考虑根的形式表示的闭环系统,
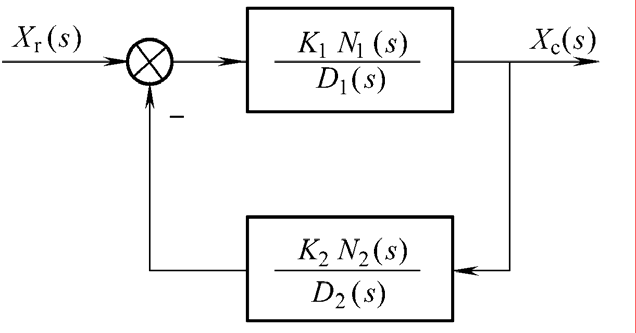
于是等效传递函数
即特征方程式
一方面,可以化为根轨迹方程
另一方面,我们把
对于复杂线性系统:梅逊增益公式
梅森公式的证明 - 知乎
(8 封私信) 自动控制原理之如何理解梅森公式(内附MATLAB求解传递函数程序) - 知乎
(8 封私信) 快速学习梅逊公式 - 知乎
(8 封私信) 模拟ic论文中各种复杂传递函数都是怎么得来的? - 知乎
自控原理应试法其三:图与梅逊公式 - 哔哩哔哩
“信号与系统界的基尔霍夫”
物理竞赛喜欢出大规模电路网络题目,往往可以用节点电流法解出。对于信号流图网络呢?
简略形式:叠加原理罢了
特征多项式的求取:啊?拓扑学吗?
多阶系统一阶化→状态空间模型
微分代数方程的状态空间方法—Wolfram Documentation
由微分方程求状态空间表达式(精) - 豆丁网
如何把高阶微分方程化成一阶微分方程组? - 知乎
《现代控制理论》之状态观测器 - 知乎
非线性系统学习笔记:(一)基础1_非线性状态空间方程-CSDN博客
CH1. 系统的状态空间模型 - 控制理论笔记 Automation
例如,MATLAB的ode45求解器只支持一阶微分方程
我要模拟下面的微分方程表示的系统,
把每一阶导数设为一个独立的状态量
化为一阶系统
于是化为一阶的向量微分方程(向量有初始值)
# 定义微分方程函数
def odefun(t, z):
dzdt = np.zeros(5)
dzdt[0] = z[1]
dzdt[1] = -z[0] - z[2] - (3*z[1])**2 + (z[3])**3 + 6*z[4] + 2*t
dzdt[2] = z[3]
dzdt[3] = z[4]
dzdt[4] = -z[4] - z[1] - np.exp(-z[0]) - t
return dzdt
指定输入量
称为状态空间方程。
可惜这不是线性系统,否则,线性系统就可以用矩阵表示了
- A是状态矩阵
- B是输入矩阵
- C是输出矩阵
- D是直接传递矩阵
于是无论多复杂的系统,都可以变成一个前向元件和一个反向元件共同作用的结果。
关于摩尔型状态机与米利型状态机的区别_状态机米勒和摩耳的优缺点-CSDN博客

【数电】时序电路的三个方程:驱动、状态、输出_数电状态方程和输出方程-CSDN博客
从数字电路得到的启发。组合逻辑电路,是次态逻辑和输出逻辑的粘连
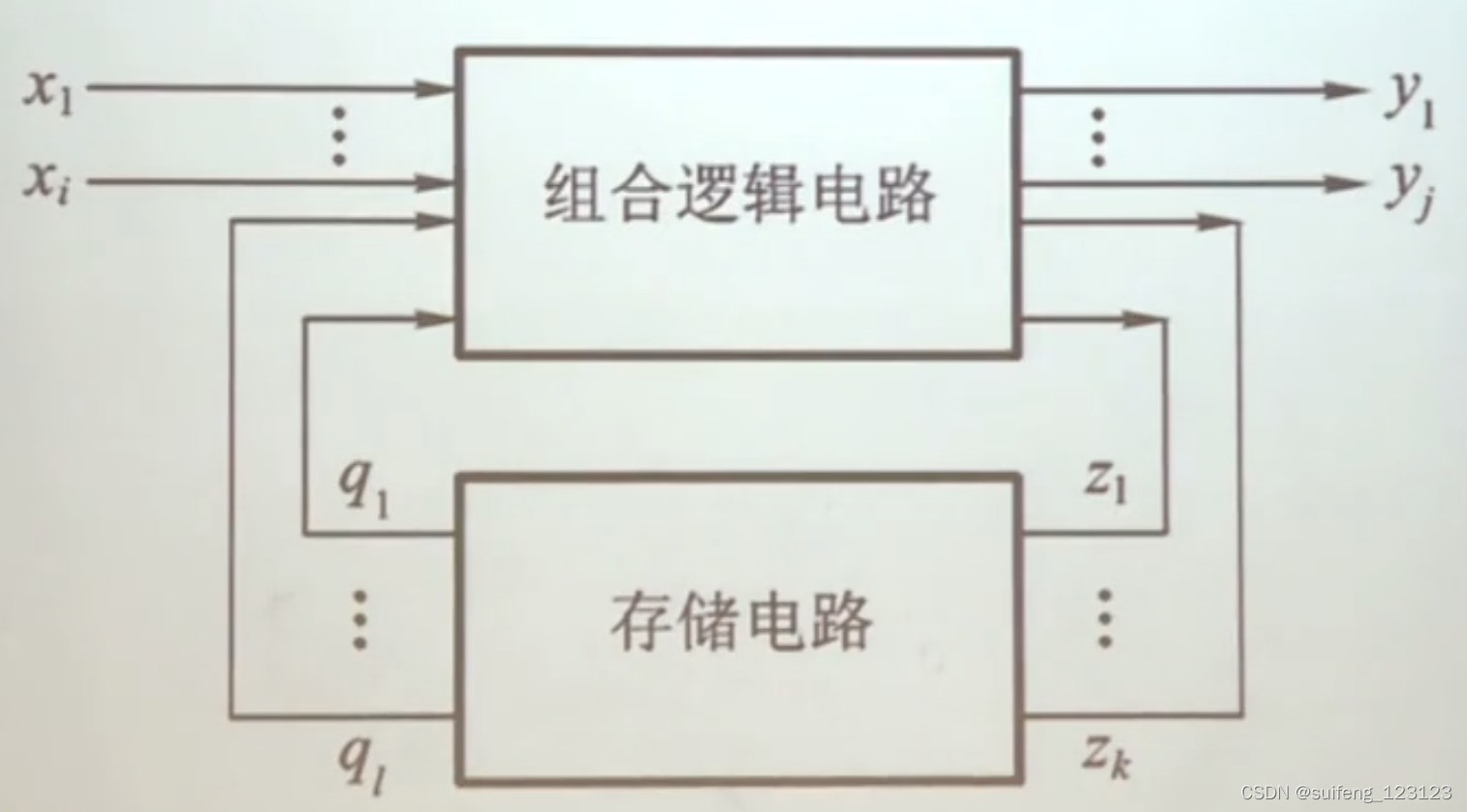
上标方括号,表示数组取元素。
状态空间模型(SSM)-CSDN博客
状态空间模型(State space midel, SSM) - 知乎
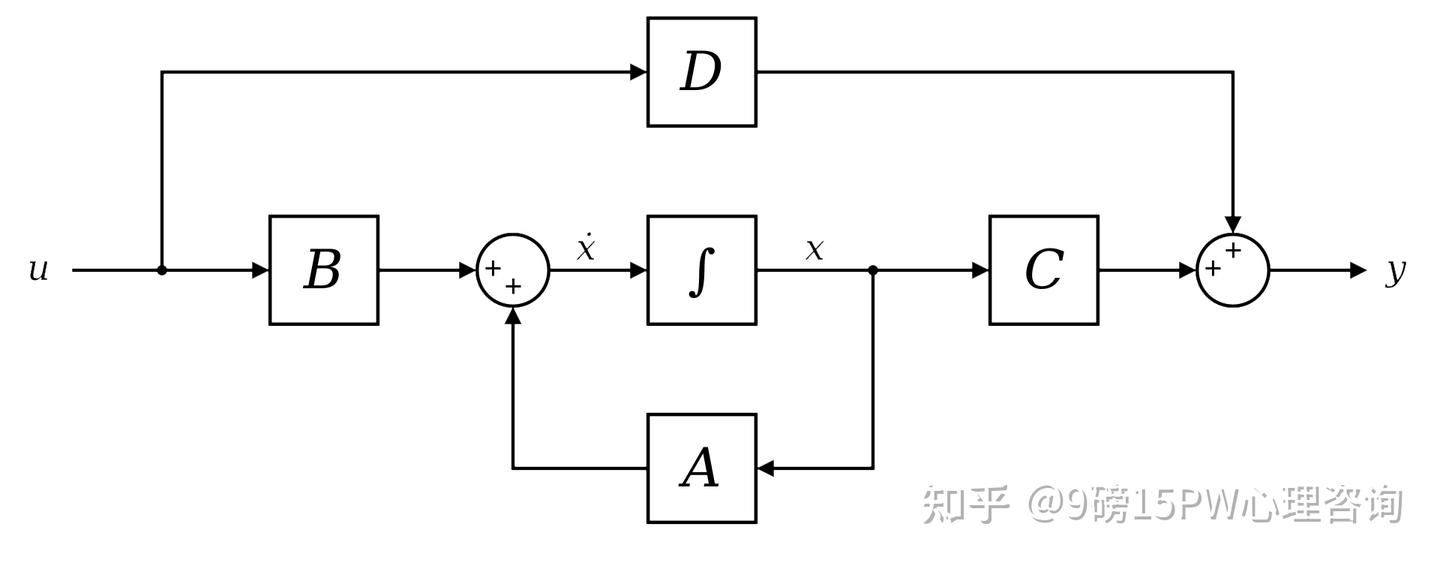
相比于时序电路,状态方程把驱动方程吸收进去了
关于摩尔型状态机与米利型状态机的区别_状态机米勒和摩耳的优缺点-CSDN博客

状态空间模型(State space midel, SSM) - 知乎
状态空间模型(SSM)-CSDN博客

摩尔型状态机,输出不受输入影响。也就是直接传递矩阵为零。
再论“特征”
如何证明矩阵指数e^At的Laplace变换是(sI-A)的逆? - 知乎
线性代数精华——矩阵的特征值与特征向量 - 知乎
证明:矩阵多项式的特征值是其特征值多项式_矩阵多项式的特征值和矩阵特征值的关系-CSDN博客
或许能用“线性微分方程的克拉默法则”为突破口,把微分方程的特征多项式和系统的、矩阵的特征多项式都串在一起!
常数变易法,就是克拉姆法则?
从状态空间方程回到传递函数,拉氏变换后解方程
解出Z,代入Y,则是(分式表示逆矩阵,I表示单位矩阵,星号是伴随矩阵)
对于输出量少于状态量的情况,即是C和D的秩比A和B更少的情况。有意思的是
这里经过了多阶系统一阶化,比经典方法多几个状态变量,传递函数的形式并没完美等价。
我们知道矩阵的特征多项式
分母
因此分析状态矩阵
相平面与相空间
只要是各个状态变量作为坐标轴的平面都可以作为相平面,无论是
交流电路的复平面可以视为相平面。
中学物理竞赛典型的“蚂蚁问题”,画出
而种群问题建模的曲线(种群数量——增长率曲线)可以视为非典型的相平面吧。
例子:二阶线性系统。过阻尼、欠阻尼、临界阻尼,相轨迹如下
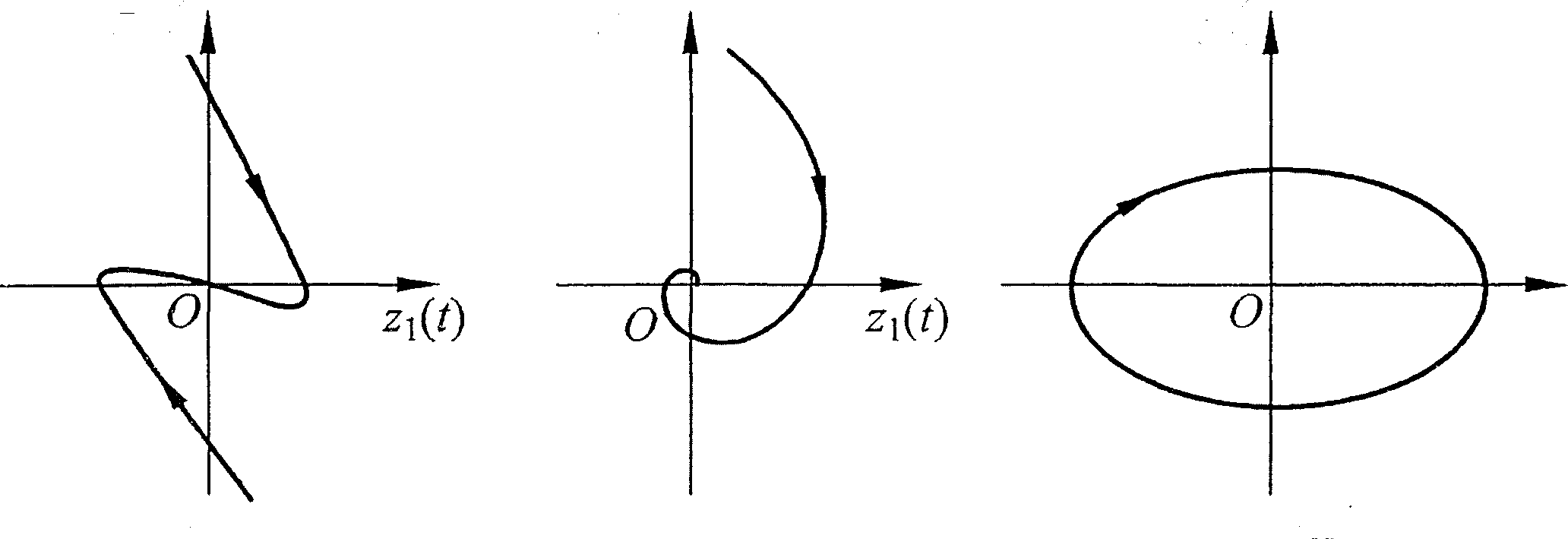
然后提一些概念。
- 相轨迹不交叉:从一个状态到另一个状态,只会有一个确定的过程,否则就是平行宇宙了
- 平衡点(奇点):相轨迹的相交点,系统抵达此处便不再运行,处于平衡状态。相轨迹在此处的切线斜率不定,即
- 特征区:人为划分的,相轨迹具有共性的区域(就像一簇一簇的纤维丛一样……)
- 调节时间:走过一段相轨迹,即从一个状态到另一个状态度过的时间
非线性系统时域近似→李雅普诺夫第一法
在 Simulink 中设计 LQR 伺服控制器 - MATLAB & Simulink
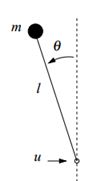
以倒立摆为例,写出状态空间方程,
简化模型:无外力输入、转动惯量
先用MATLAB看一看相轨迹吧
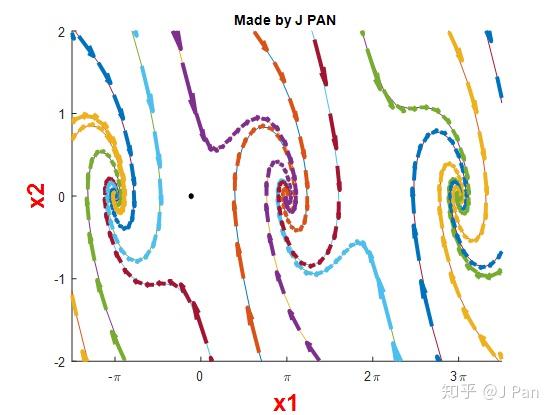
对于特定的平衡点,不考虑稳定性,自然可以直接令导数为零求解
得到平衡点
李雅普诺夫第一法:线性近似
倒立摆系统显然是非线性系统
李雅普诺夫第一法就是在微扰动情况下把非线性方程线性化。现在我们以已知平衡点
非线性方程近似为
非线性系统频域近似→描述函数(谐波平衡法)
本质非线性:不连续的非线性,饱和、死区、开关、间隙、滞后、奇怪的间断点
非本质非线性:连续的非线性,只是直线变成了曲线
描述函数法是一种近似方法,相当于线性理论中频率法的推广。方法不受阶次的限制。
设非线性系统可以拆分成线性元件和非线性元件,如图(串联顺序也可能相反)
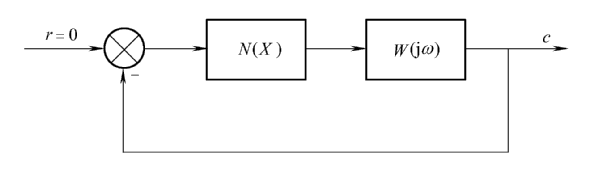
描述函数是对非线性特性在正弦信号作用下的输出,进行谐波线性化处理之后得到的
稳定性分析
时域响应分析
阶跃响应,即目标量突变,系统对这个情况的行为
例子:一个电容,此前没有电量,然后立即充电
例子:一个弹簧,此前用手压缩,然后立即松开
时域响应分析,其实就是用拉普拉斯法(算子法)解微分方程的过程。
BIBO稳定性判据
信号与系统:BIBO稳定性判据 - 技术教程
有界输入有界输出稳定性-数学百科
根的判据
高等代数(二)预习——4、唯一因式分解定理 - Halifuda - 博客园
典型二阶系统的时域动态特性可知,稳定性还是要看特征根在平面的位置
时,系统的极点均位于左半平面, ,系统的动态过程呈现指数衰减或衰减振荡,系统是渐进稳定的; 时,系统的极点位于右半平面, ,系统的动态过程呈现发散振荡,系统是不稳定的; 时,系统的极点位于虚轴, ,系统的动态过程呈现等幅振荡,系统是李雅普诺夫意义下的稳定的。
对于高阶系统传递函数,都可通过因式分解拆分成多个一阶系统和二阶系统。
解微分方程可得
因此对于高阶系统,关键看极点的实数部分
- 所有极点位于左半边,衰减,渐进稳定;
- 存在极点位于右半边,发散,不稳定;
- 存在极点位于虚轴,振荡或趋于常数(稳态误差),李雅普诺夫意义下稳定。
也可以把多阶微分方程一阶化状态空间方程的形式,发现状态矩阵(应该是赫尔维茨矩阵,下面来探讨)
特征值判据
周彬《线性系统理论》第3章3.2节:稳定性直接判据 - 知乎
CH1. 系统的状态空间模型 - 控制理论笔记 Automation
矩阵指数 - 知乎
线性系统的状态空间方程通过矩阵微分方程求解,可以变成这样(推导略)
因此对于状态空间方程,关键看状态矩阵
- 特征值实部全为负,衰减,渐进稳定;
- 特征值实部存在正,发散,不稳定;
- 存在特征值实部为零,振荡或趋于常数(稳态误差),李雅普诺夫意义下稳定。
也可以把状态空间方程还原成矩阵传递函数的形式,发现特征多项式即为
劳斯——赫尔维茨判据
1.5~1.6赫尔维茨多项式、劳斯–赫尔维茨判定 - 知乎
(十三)判断稳定性:劳斯判据 - 知乎
赫尔维茨定理_百度百科
二次型与正定性 - 知乎
线性代数学习笔记——第六章学习指南——二次型与二次曲面_根据二次型求对应曲线的方法-CSDN博客
6 二次型与二次曲面
《常微分方程及其稳定性》(二) - 知乎
Routh-Hurwitz准则——判别实系数多项式有无实部非负的根的充要条件 - 知乎
劳斯–赫尔维茨稳定性判据-数学百科
劳斯阵列的推导-数学百科
第四章-控制系统的李雅普诺夫稳定性分析 | EpsilonJohn's Blog
哈尔滨工程大学刘胜的自动控制原理,书后附录有证明,当然我觉得还可以看看原论文,现在书上应该会列出参考文献
从状态空间方程到状态转移矩阵,和从传递函数到特征多项式的赫尔维茨矩阵,殊途同归于“判断矩阵正定性”,但是
到这里证明就难了,虽然也是对于正定性的判断,但是对于特征方程,已经丢失了很多信息
赫尔维茨矩阵(转置后写法)
赫尔维茨行列式
这个n阶行列式的构造方法如下:
- 在主对角线上,从
开始依次写入特征多项式系数,直至 为止。 - 在每一列内从上到下按下标递减的顺序填入其他系数。
以下用0补齐。 - 或者从另一个角度看待,135、024……奇数项和偶数项分列排开。
赫尔维茨稳定判据:特征方程式的全部根都在左半复平面,的充分必要条件是,上述行列式的各阶主子式均大于0——赫尔维茨矩阵是正定矩阵。
我们经常使用矩阵的正定性判断二次型(二次曲面)的“形状”。
在这里我们拿它来判断二次方程的根的分布,估计是可以通过状态空间方程法把多项式降阶。
劳斯表和劳斯判据可以简化运算。
用劳斯表表示:
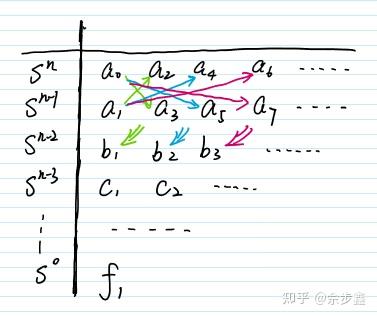
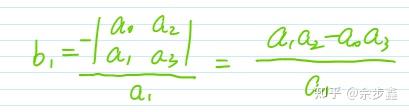
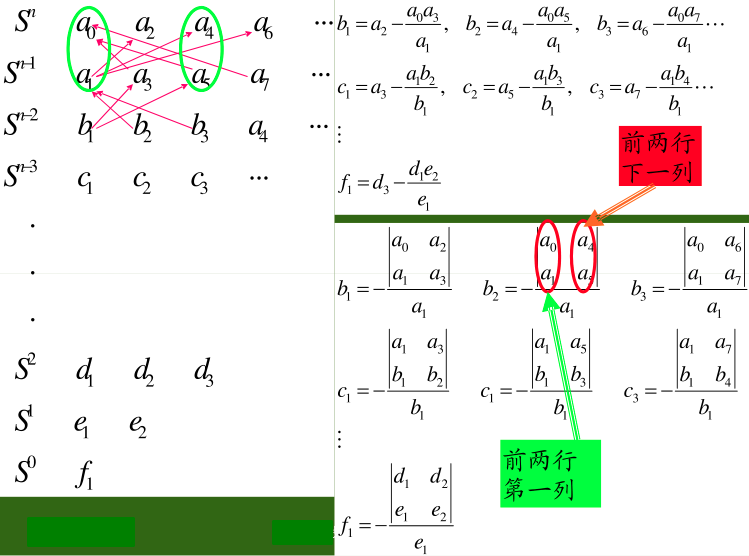
劳斯判据:特征方程式的全部根都在左半平面的充分必要条件是劳斯表的1列系数全部是正数。
谢绪恺——聂义勇判据
根全部具有负实部的必要条件为
根全部具有负实部的充分条件为
频域响应分析
【东大自控笔记10】频域分析方法(幅相特性曲线与对数频率特性曲线[伯德图])对数幅相特性曲线mr-CSDN博客
复阻抗法 求解 传递函数_复阻抗法求传递函数-CSDN博客
引理:对于线性时不变系统,输入复指数量(正弦波),输出频率相等的复指数量(正弦波)
傅里叶变换的微分性质和复指数函数的微分性质形式相似
对复指数量取微分,
等式两端取变换,
这么一搞,无论是
于是,输出量的复数表示的比值、输出量的频域表示的比值,恰好相等,正是传递函数(
奈奎斯特判据
(9 封私信) 怎么通俗理解 Nyquist 稳定判据? - 知乎
放大器的传递函数基础、幅值裕度 & 相位裕度的概念 - 知乎
考虑一个闭环系统,仍然根据:系统稳定的充分必要条件是闭环传递函数的极点均在 s 左半平面
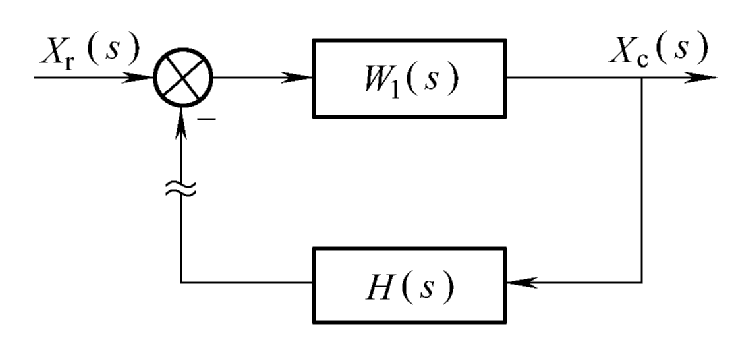
奈奎斯特辅助函数 F(s) 和传递函数一样,是一个对复数的映射,从复数域映射到复数域。
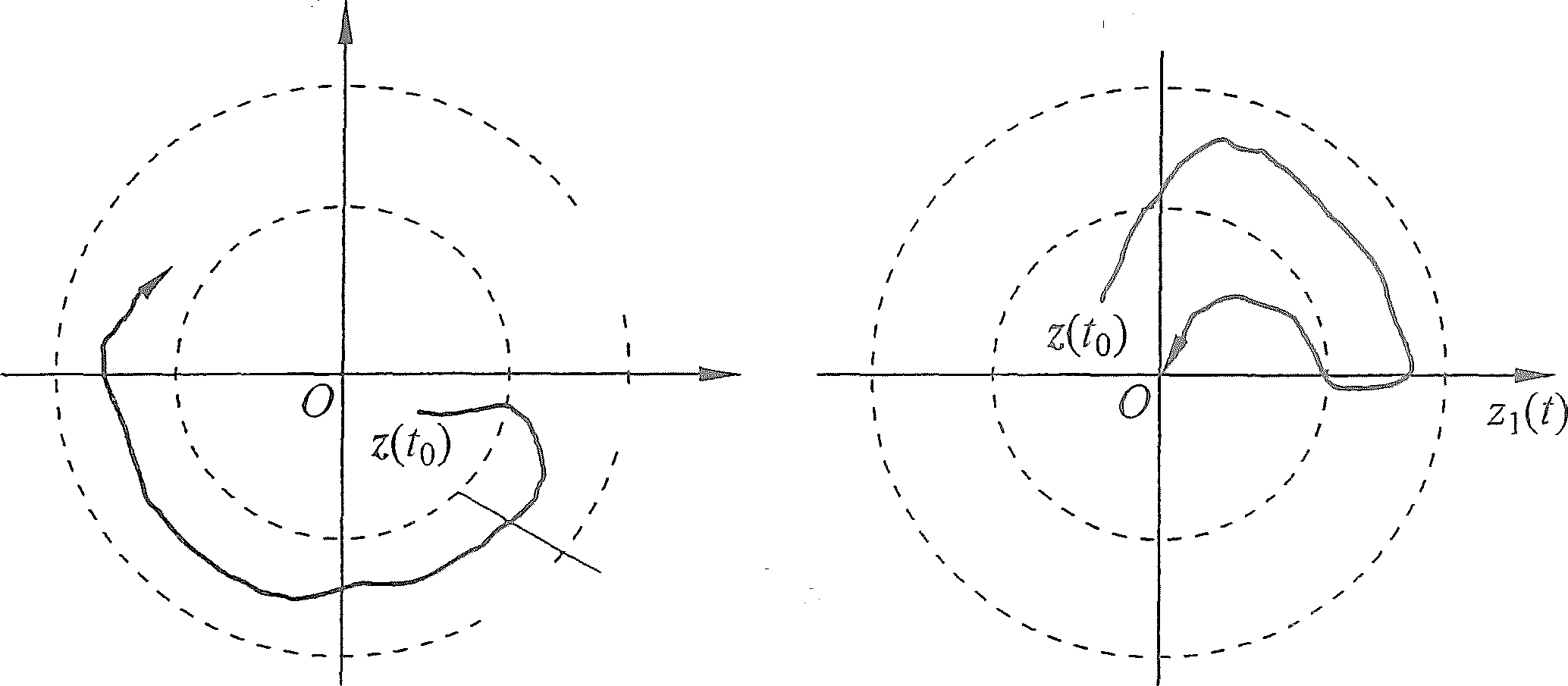
映射定理:在 s 平面上如闭合路径顺时针包围 F(s) 的P 个极点、Z 个零点,则在 F(s) 平面上对应有一条闭合路径围绕原点逆时针旋转的圈数为N, 则有 N=P-Z
用留数法可以理解,例如在s顺时针包围一个极点,在F(s)就顺时针包围无穷远点,等价于在F(s)逆时针包围原点。
奈氏稳定判据一:如果开环系统是稳定的,那么闭环系统稳定的条件是:当
奈氏稳定判据二:如果开环系统是不稳定的,开环系统特征方程式有P个根在右半s平面上,则闭环系统稳定的充要条件是:当
围绕
由于奈奎斯特判据的关键点在
相位裕度:规定当
增益裕度:规定当
稳定系统的稳定裕度
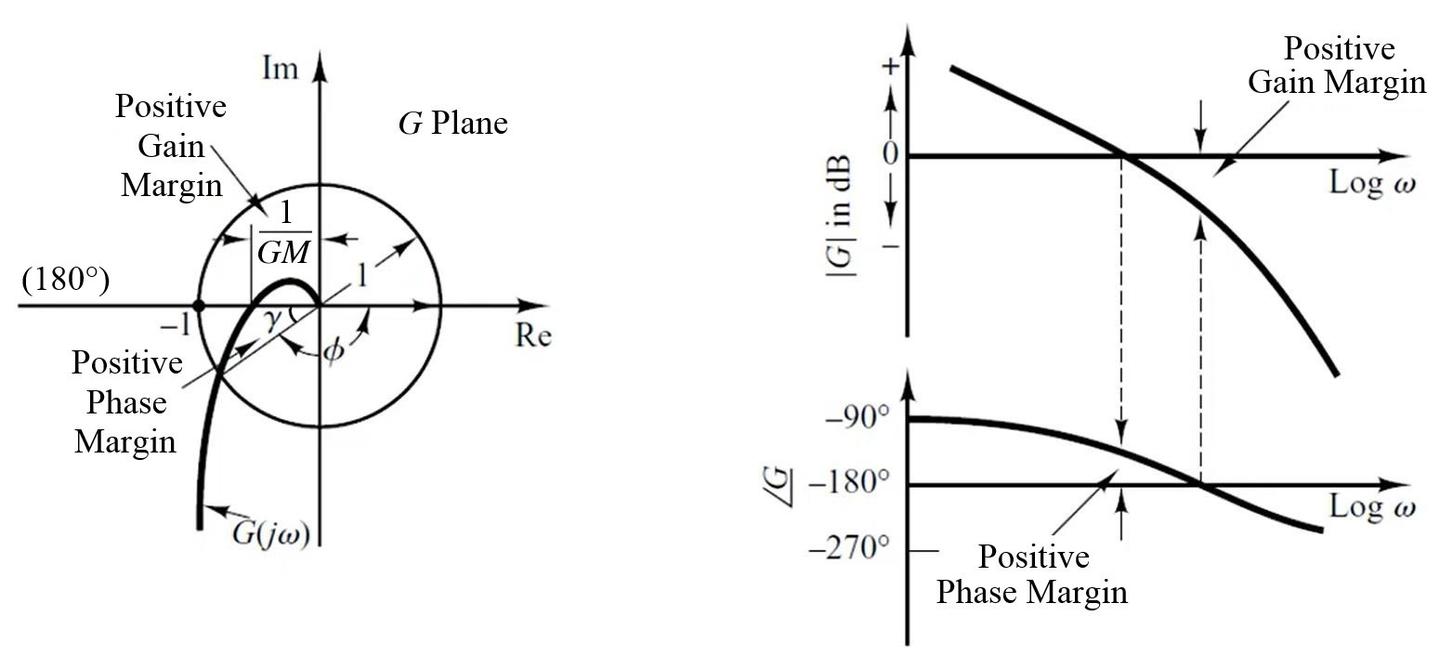
不稳定系统的稳定裕度
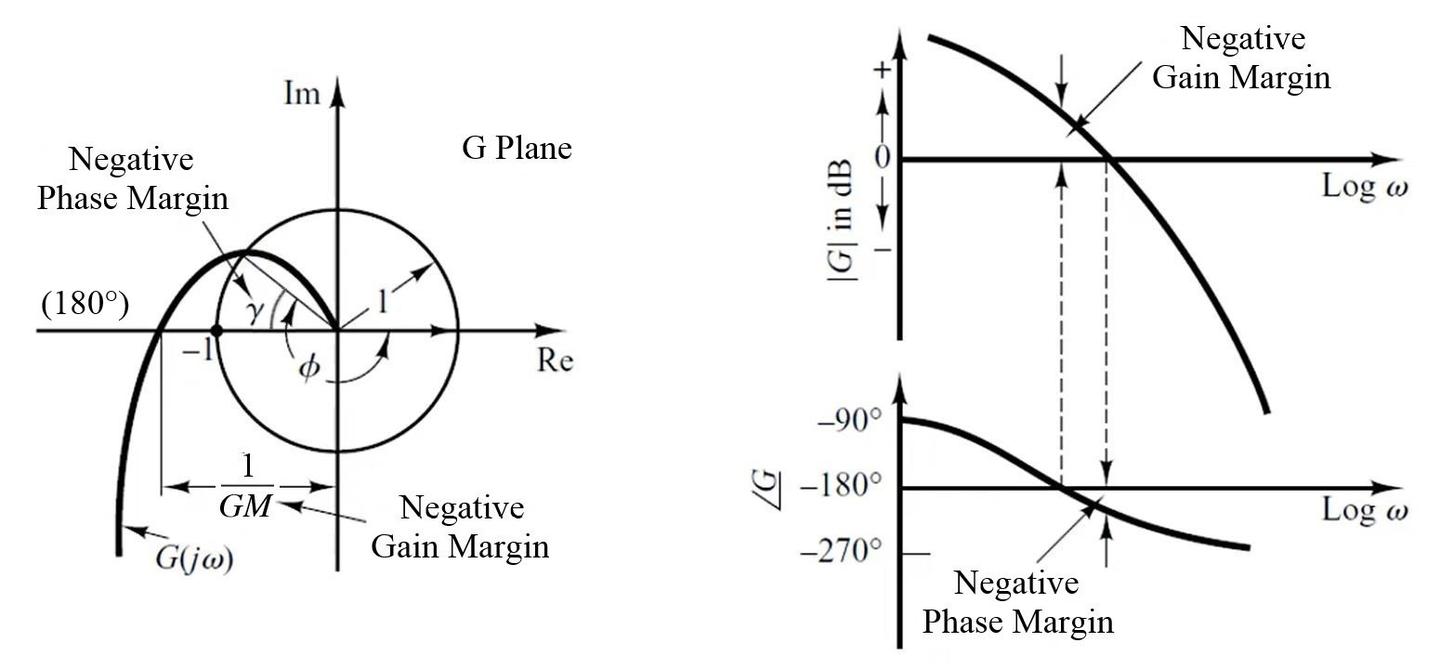
伯德图判据
广义能量分析
现代控制理论——稳定性分析(Lyapunov) - 知乎
现代控制理论—非线性控制—Lyapunov直接方法 - 知乎
李雅普诺夫稳定性理论(万字长文,全网最全!) - 知乎
PowerPoint 演示文稿
Hessian 矩阵的正定性与目标函数凸性的证明_hessian矩阵判断凸函数-CSDN博客
Hessian矩阵与函数的凹凸性(学习笔记) - 知乎
《常微分方程及其稳定性》(二) - 知乎
第三章——Lyapunov理论基础_lyapunov函数-CSDN博客
李雅普诺夫直接法/第二法
预备知识:函数性质
函数的正定性(应该就是凹凸性吧):
- 正定 (positive definite), 若
- 半正定 (positive semi-definite), 若
- 负定 (negative definite), 若
- 半负定 (negative semi-definite), 若
- 不定 (indefinite), 若其可正可负。
这么说的话,可以根据原点Hessian矩阵的正定性推断函数的正定性。
函数的径向无界性:
若引入时间量,如
笛卡尔乘积_百度百科
乘积A×B是一个新的集合,包含了所有可能的有序对 (a, b),其中a∈A,b∈B。
开始构造:能量函数
李雅普诺夫函数 - 维基百科,自由的百科全书
如何构建李雅普诺夫方程(或者说有什么构建方程的技巧吗)? - 知乎
构造一个标量函数——能量函数,满足规定
- 正定函数(除 x=0 外严格为正)
- 以 t 为自变量时单调下降,
这两个规定,是为了证明稳定性做准备的,不满足这两个规定的函数不可能对我们有帮助。
李雅普诺夫主稳定性定理,让我们考虑两个量
- 候选函数
- 候选函数的时间导数
| 李雅普诺夫稳定 | 邻域内 | |||
| 渐近稳定 | 邻域内 | |||
| 全局李雅普诺夫稳定 | 整个空间 | |||
| 全局渐近稳定 | 整个空间 |
若要证明一致稳定性,要让
1.
2.
这样系统也是渐进稳定的
如果我们定义李雅普诺夫函数(瞪眼法,就像积分因子法解微分方程一样瞪)
验证
显然当
形象地思考:位置上正定,势能是凹的;速度上负定,动能是凸的
如果能合理的选定李雅普诺夫函数,则非常容易的判断系统的稳定性。
不过遗憾的是,对于复杂的系统,李雅普诺夫函数的选择或者说寻找可以称得上一门玄学。
构造李雅普诺夫函数的方法:凑合Lyapunov函数法、倒推Lyapunov函数法、Krasovski方法
所以,对于工程师而言,还是喜欢李雅普诺夫第一法。
对于线性时不变系统:赫尔维茨矩阵与李雅普诺夫方程
线性系统(Linear Systems)—3.6 线性定常系统的稳定性 - 知乎
线性代数 | 李雅普诺夫方程
最优控制公式推导(代数里卡提方程,李雅普诺夫方程,HJB方程)最优控制are-CSDN博客
线性时不变系统用状态矩阵表示
其通解为
线性定常系统的零解是
- Lyapunov 稳定的, 当且仅当
, 且若 ,则 。 - 全局(一致)渐近稳定的,当且仅当
。赫尔维茨矩阵! - 全局(一致)指数稳定的, 当且仅当
。
当
A 称为 Hurwitz 矩阵,当且仅当:
对任给的正定对称矩阵 Q, 存在满足 Lyapunov 方程
换句话说,若存在正定矩阵P满足
充分性 线性定常系统的渐近稳定性等价于存在一个二次型的 Lyapunov 函数,可以就此把 Lyapunov 函数确定出来。
必要性 考虑如下矩阵微分方程和它的解
对矩阵微分方程积分
配凑李雅普诺夫方程形式,构造
只需证明
且
波波夫超稳定性理论
控制器校正
观测器
(7 封私信) 【现代控制理论】状态观测器——龙伯格观测器(Luenberger observer) - 知乎
【现代控制理论笔记】——第六章:状态观测器-CSDN博客
基本性质
[现代控制理论2-4(2)] 系统能观性分析 - 知乎
线性系统理论(三)能控性与能观性 - 知乎
强化学习与状态
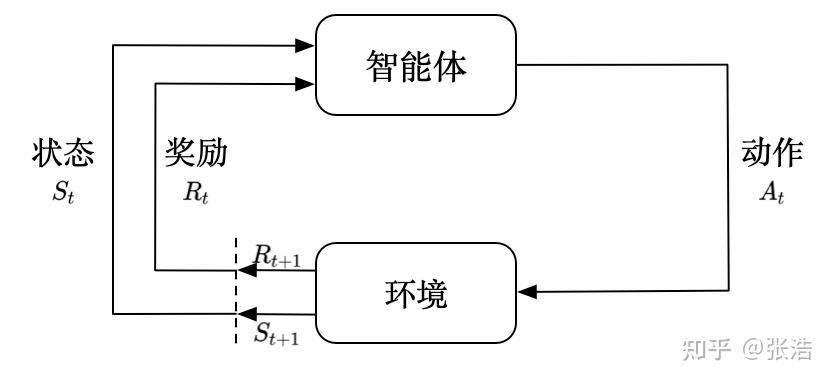
控制器就是智能体
状态空间模型是描述环境或智能体的有力手段。以环境作研究对象为例
- 状态
是观测方程(观测通常表示不完整输入) - 动作
是输入变量
奖励是评判学习的指标,平常其实不该是传给智能体本身的,而是只有在训练框架下起作用
随机微分方程与随机系统
概率状态空间模型
#概率状态空间模型
滤波估计理论(一)——贝叶斯滤波_bayesian filtering and smoothing-CSDN博客
随机控制理论_百度百科
任何设备都有不确定性(物理实验中叫不确定度),于是我们从条件概率的视角看待状态空间模型
行业黑话:在概率模型中,波浪线符号“∼”通常表示“服从某种分布”
即 xₖ 的取值由给定过去状态 x₀:ₖ₋₁ 和过去观测 z₁:ₖ₋₁ 的条件分布生成。
即 zₖ 由当前状态 x₀:ₖ 和过去观测 z₁:ₖ₋₁ 的条件分布生成。
p是一种分布,本质上也是概率构成的一个函数,而函数的本质可以是序列
简化成隐马尔可夫模型:
- 状态
只和前一个给定时刻状态有关(马尔可夫性) - 量测
只和当前状态有关(条件独立性)
即
顺序数据:状态空间模型_状态空间模型(state space models,ssm)举例说明-CSDN博客
这其实是一个马尔可夫链

