Summary

评价器。相较于分类器，很多评价器也是基于加权求和，但是根本没有现有答案来对数据分类（没有已知评价），所以相比于做正确的决定，更像是猜应当的决策
所以说，这是没有现成答案可训练的数据降维方法。所以像是“这个元件只负责数据规约，规约并不存在理想答案”
下面的很多方法，只是在赋权，而不是通过目标函数求取权重。
还有不基于权重的方法（TOPSIS），但仍旧是数据规约的一种。

数据预处理(五)——数据规约-CSDN博客
 决策、优化和规划的区别，较详细的思维导图理清这一切！优化算法和规划算法的区别-CSDN博客
 决策、优化和规划的区别，较详细的思维导图理清这一切！ - 知乎
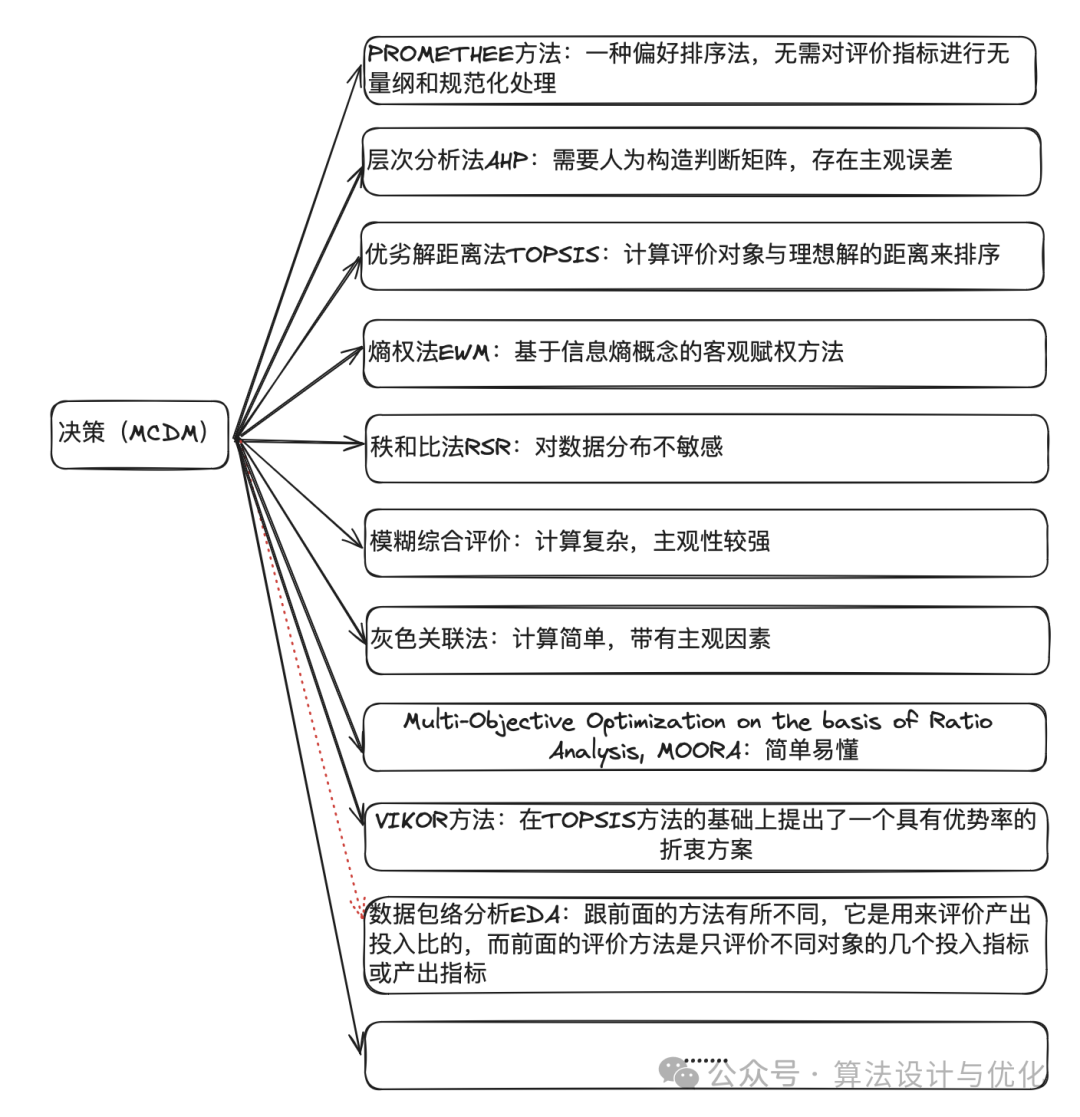
Pasted image 20250720022750.png

看权重！
德尔菲法
看产能（Pareto最优解构成的生产前沿面）！
数据包络
确定吗？
模糊综合评价

基于丢弃的方法

也就是把指标集中在一处（也可能是降维构造的新指标），其他指标丢弃，即权重为零

低方差过滤

先将变量进行归一化，当变量方差足够小时，那么认为，这个变量携带的信息比较少少。
设定阈值，当变量的方差小于阈值时，去掉即可。

基于权重的方法

层次分析法相对赋权

数学建模笔记——评价类模型（一） - 简书
 用人话讲明白AHP层次分析法（非常详细原理+简单工具实现）如何用spss做ahp层次分析-CSDN博客
 层次分析之算术平均法、几何计算法、特征值法计算权重 matlab实现_几何平均法求权重-CSDN博客

层次分析：把一些指标放在同一层比较，另一些指标放在另一层比较，因此得名。

对于多个指标，我们可以两个两个进行比较评价，根据两两比较的结果来判断权重。为了进行量化，层次分析法使用了九个等级18个数字来比较两个指标之间的重要性（满意度），如下图。

为了记录这些关系，构成判断矩阵A，里面的元素就作为参数。（用矩阵表示两两关系，有点像邻接矩阵）

“一致矩阵”，也就是都要满足 $a_{i k} = a_{i j} \cdot a_{j k}$ ，重要性比例可以传递，且不要出现“石头剪刀布”一样的回环情况。如图，不一致矩阵和一致矩阵

下面进行一致性检验。基于如下引理

计算一致性指标 $C I = \frac{λ_{m a x} - n}{n - 1}$ ，其中 $λ_{m a x}$ 为判断矩阵最大的特征值（如果特征值中有虚数，比较的是特征值的模长）， $n$ 是判断矩阵的阶数。

查找对应的平均随机一致性指标RI，直接查表就好了

计算一致性比例 $C R = \frac{C I}{R I}$ ，之后就可以下判断了，如果CR<0.1，则认为判断矩阵的一致性可以接受，否则需要对判断矩阵进行修正，也就是尽量往一致矩阵去调整。

得到判断矩阵后，可以通过三种不同的方法求权重。

算术平均数求权重：取一列/一行向量作为权重，并进行归一化。每一列应该都有一个权重，那怎么取舍呢？很自然的想法就是取平均数嘛。总结起来就是下面的步骤
- 按行相加得到一个新的列向量
- 将向量的每个分量除以n
- 对该列向量进行归一化即可得到权重向量
- 另外，如果判断矩阵是一个一致矩阵，同一指标在每一列的权重都是相同的，可以直接取其中一列进行归一化
几何平均数求权重
- 按行相乘得到一个新的列向量
- 将向量的每个分量开n次方
- 对该列向量进行归一化即可得到权重向量
特征值法求权重
- 求出特征向量W，即AW=λW，对特征向量归一化即可得到权重

变异系数法

多指标综合评价算法 - 多指标综合评价算法（一）：变异系数法 - 《算法博客》 - 极客文档
变异系数：标准差除以均值

\begin{array}{r} V_{i} = \frac{σ_{i}}{{\bar{x}}_{i}} (i = 1, 2, \dots, n) \end{array}

权重：变异系数占比

\begin{array}{r} W_{i} = \frac{V_{i}}{\sum_{i = 1}^{n} V_{i}} \end{array}

熵权法

最常用的客观赋权方法——熵权法_客观赋权法-CSDN博客
 多指标综合评价算法 - 多指标综合评价算法（二）：熵权法 - 《算法博客》 - 极客文档
 数学建模笔记——评价类模型之熵权法 - 简书
熵越小，负熵越大，信息越多（说明本身的变异程度就很大）
熵越大，信息越少（说明本身变异程度很小，没什么指导性，巨大的可能性）
于是根据熵来赋权，熵与权负相关

先写出香农熵公式

H (x) = - \sum_{i = 1}^{n} [p (x_{i}) l n (p (x_{i}))]

看看熵权法步骤吧

数据归一化。原始数据矩阵为X，归一化数据矩阵为Y， $max (\vec{x})$ 为向量中的一个最大元素

\begin{array}{r} y_{i j} = \frac{x_{i j} - min ({\vec{x}}_{i})}{max ({\vec{x}}_{i}) - min ({\vec{x}}_{i})} (正向指标), y_{i j} = \frac{min ({\vec{x}}_{i}) - x_{i j}}{max ({\vec{x}}_{i}) - min ({\vec{x}}_{i})} (负向指标) \end{array}

视比率为概率并计算。设某一级指标有m个二级指标（属性），且已取得n年数据，记为矩阵 $Y_{i j}$ 。在同一指标（属性）下，计算出各年取值占全部年值和的比重

p_{i j} = \frac{y_{i j}}{\sum_{i = 1}^{n} y_{i j}} (i = 1, 2, \dots, n; j = 1, 2, \dots, m)

计算第j项指标（属性）的信息熵，每一项都算。归一化：当 $p (x_{1}) = p (x_{2}) = . . . = p (x_{n}) = \frac{1}{n}$ 时， $H (x)$ 取最大值为 $\ln (n)$ ，所以我们计算 $E_{j}$ 时，除以一个常数 $\ln (n)$ ，可以使 $E_{j}$ 的范围落在 $[0, 1]$ 之间。

E_{j} = - \ln (n)^{- 1} \sum_{i = 1}^{n} p_{i j} \ln p_{i j} (若 p_{i j} = 0, 定义 E_{j} = 0)

计算权重，按如下公式。这里k指的是指标个数，即k=m，不是什么玻尔兹曼常量！

\begin{array}{r} 定 义 ， 信 息 效 用 值 （ 信 息 冗 余 度 ） D = 1 - E \\ 则 w = \frac{D}{\sum D}, w_{j} = \frac{1 - E_{j}}{k - Σ E_{j}}, k 是 指 标 个 数 \end{array}

加权的综合评分就可以这样计算了

s_{i} = \sum_{j = 1}^{m} w_{j} \cdot x_{i j}

灰关联系数赋权

灰色关联算法原理与实现详解 - 知乎
 灰色关联度分析（Grey Relation Analysis，GRA）原理详解[通俗易懂]-腾讯云开发者社区-腾讯云
 数学建模笔记——评价类模型之灰色关联分析 - 简书
 数据变换方法: 初值化、均值化、百分比/倍数变换、归一化、极差最大值化、区间值化： MinMaxScaler、StandardScaler、MaxAbsScaler-CSDN博客
先进行灰色关联分析，再根据分析出的关联系数确定权重。

灰关联系数

先上公式

ζ_{i} (k) = \frac{min_{i} max_{k} | x_{0} (k) - x_{i} (k) | + ρ \cdot max_{i} max_{k} | x_{0} (k) - x_{i} (k) |}{| x_{0} (k) - x_{i} (k) | + ρ \cdot max_{i} max_{k} | x_{0} (k) - x_{i} (k) |}

这是在干什么？

首先，ρ是一个可调的系数； $x_{0}$ 是母指标，参考序列，是我们研究的反映特征（类似于自变量）； $x_{i}$ 是子指标，比较序列，是我们研究相关性的影响特征（类似于因变量）。
$| x_{0} (k) - x_{i} (k) |$ ，就是两个序列在k时刻的差距，关于k变化，关于i变化
$max_{k} | x_{0} (k) - x_{i} (k) |$ ，也就是两个序列找其中的差距最大值，关于k恒定，关于i变化
$min_{i} max_{k} | x_{0} (k) - x_{i} (k) |$ ，在多个序列的差距最大值里面找最小，也就是最贴近的序列的最大差距，关于k恒定，关于i恒定
再把公式缩写一下

ζ_{i} (k) = \frac{Δ_{min} x + ρ Δ_{max} x}{Δ x (k) + ρ Δ_{max} x}

对于最贴近的序列的最遥远的点， $ζ = 1$ ；对于更贴近的点， $ζ > 1$ ；对于更遥远的点， $ζ < 1$
为什么这么写？ $Δ_{min} x$ 是可能为零的， $ρ Δ_{max} x$ 是一个偏置；这有点像糖水稀释， $ρ$ 取得越大，不同 $ζ$ 系数的差距就越小。

为什么？

听说灰色关联分析方法要求样本容量可以少到4个，对数据无规律同样适用，不会出现量化结果与定性分析结果不符的情况

步骤

对于一组序列

对序列的去量纲化。方法有很多，任选：初值化、均值化、百分比化、倍数化、区间归一化、极差最大值化
用公式，代入不同指标的不同时刻，计算灰关联系数序列。
关联度：计算各个灰关联系数序列的均值，即 $r_{0 i}^{r} = \frac{1}{m} \sum_{k = 1}^{m} δ_{i} (k)$
根据关联度占总关联度的比重计算权重，即 $w_{i} = \frac{r_{i}}{\sum_{j = 1}^{m} r_{j}}$
加权的综合评分就可以计算了

TOPSIS

数学建模笔记——评价类模型（二） - 简书

一句话

评 分 = \frac{某 一 方 案 - 最 劣 解}{理 想 最 优 解 - 最 劣 解} \to 评 分 = \frac{与 最 劣 解 的 距 离}{与 最 优 解 的 距 离 + 与 最 劣 解 的 距 离}

前者直观明了，就是评分的一个归一化；在一维状态下，前者与后者等价
但后者才是数据降维，把更高维的度量状况评分为一维指标。
这个转变，以欧氏距离为例，变形前后分母的计算结果其实是不同的，从定值变成了纳入考量的动值。（我们衡量的得分是考虑到某个方案距离最优解和最劣解的一个综合距离，且不同度量下的空间特性不同，不考虑最劣解的距离，说明不充分）

[QUESTION]
哎？这或许就是灰色关联系数定义的思路来源

实际中方案根本不能做差，怎么办呢？

正向化处理：有些指标的数据越大越好，有些则是越小越好，有些又是中间某个值或者某段区间最好。我们可以对其进行“正向化处理”，使指标都可以像考试分数那样，越大越好。
- 极小型指标，例如费用，争吵次数，我们可以用 ${\hat{x}}_{i} = m a x - x_{i}$ 将其转化为极大型，如果所有元素都为正数，也可以使用 ${\hat{x}}_{i} = \frac{1}{x_{i}}$ 。
- 中间型指标，如果其最佳数值是 $x_{b e s t}$ ，我们可以取 $M = m a x {| x_{i} - x_{b e s t} |}$ ，之后按照 ${\hat{x}}_{i} = 1 - \frac{x_{i} - x_{b e s t}}{M}$ 转化。
- 对于区间型指标，如果其最佳区间是 $[a, b]$ ，我们取 $M = m a x {a - m i n {x_{i}}, m a x {x_{i}} - b}$ ，之后按照 ${\hat{x}}_{i} = {\begin{cases} 1 - \frac{a - x_{i}}{M}, & x_{i} < a \\ 1, & a < x_{i} < b \\ 1 - \frac{x_{i} - b}{M}, & x_{i} > b \end{cases}$ 转化。
对已经正向化的矩阵进行标准化，消除量纲影响。
- 在概率统计中，标准化的方法一般是 $\frac{X - E X}{\sqrt{D X}}$ ，不过也可以用别的办法。
- 用这种方法标准化也可以：我们记标准化后的矩阵为 $Z$ ，其中 $z_{i j} = \frac{x_{i j}}{\sqrt{\sum_{i = 1}^{n} {x_{i j}}^{2}}}$ ，也就是 $\frac{每一个元素}{\sqrt{其所在列的元素的平方和}}$
现在，我们已经得到了标准化的数据矩阵。可以拿 $\frac{| {\vec{z}}_{i} - {\vec{z}}_{m i n} |}{| {\vec{z}}_{m a x} - {\vec{z}}_{i} | + | {\vec{z}}_{i} - {\vec{z}}_{m i n} |}$ 来评分啦。

数据包络分析

基于投影的方法

特征工程 - 数据规约 - paramotor - 博客园

在高维空间的数据，位于或接近低维子空间，将这些数据投影到该子空间。

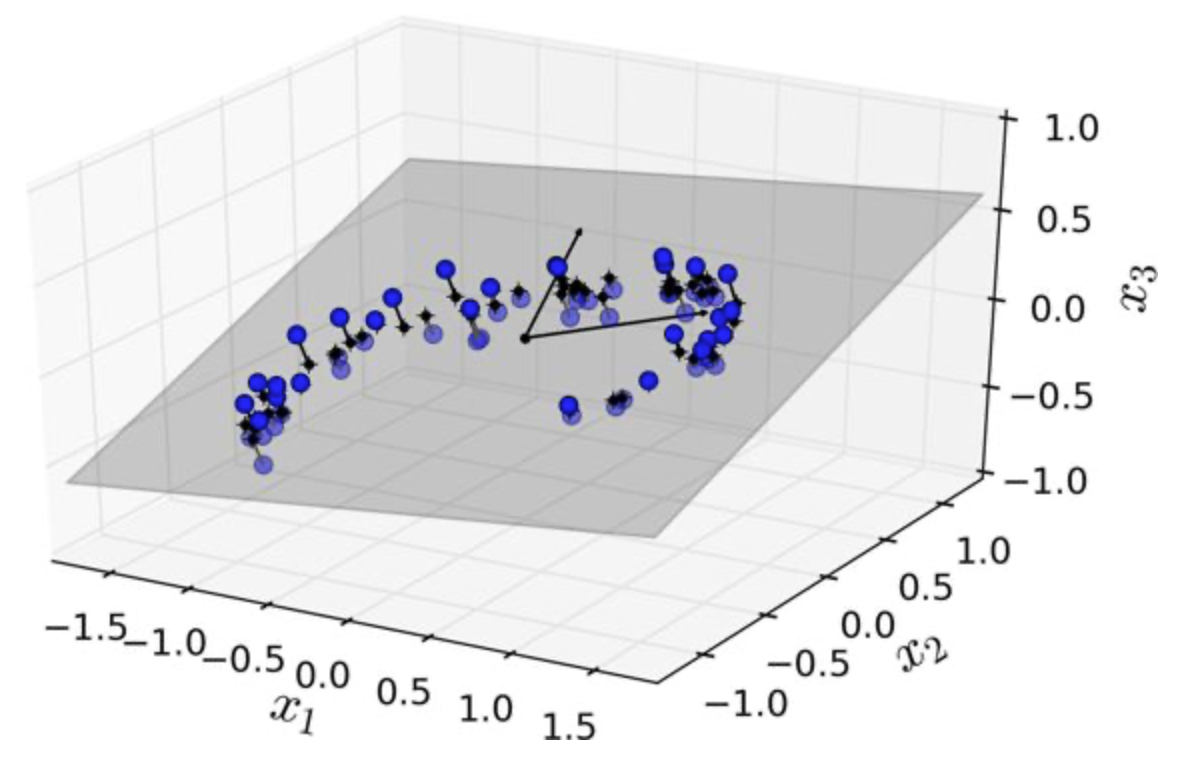
主成分分析

在低方差过滤之前，先进行坐标变换（协方差矩阵的特征分解），按照方差极值方向来计算方差

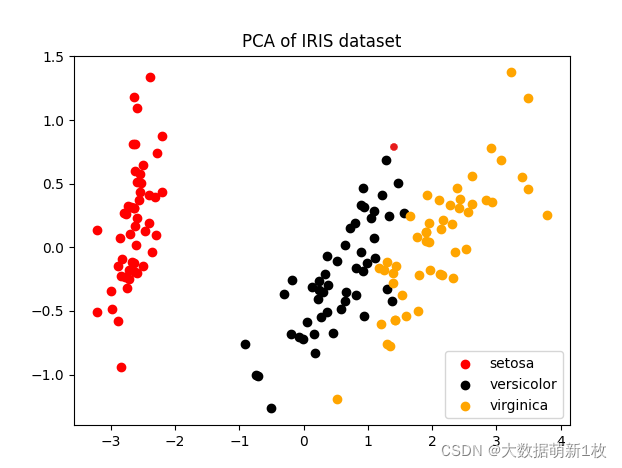
如图，原数据是4维的鸢尾花数据集，通过PCA降至2维。

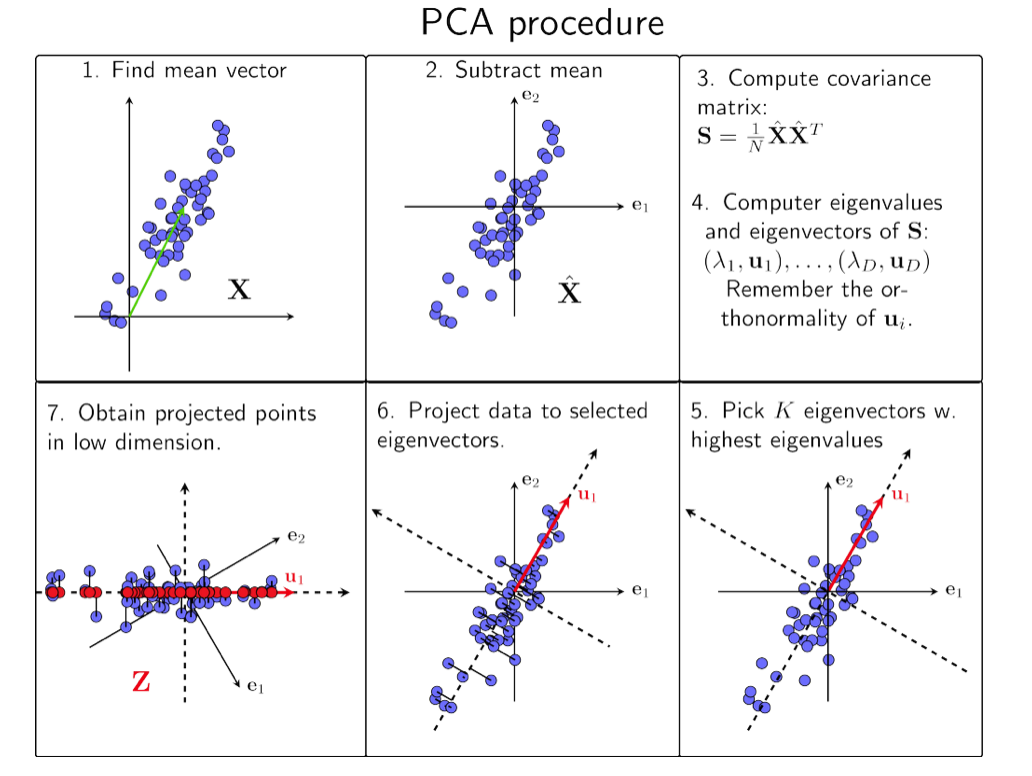
如图，2维数据，通过PCA最终得到1维数据，既左下角的红点。

主成分分析PCA步骤如下：

原始数据（点云）坐标变换到质心（全体减去均值，以均值为坐标原点）
计算点云的协方差矩阵并特征分解 $U^{T} Λ U$ （特征向量与特征值，表示方差在此方向得到极值）
维度 $k$ 自选，观察 $Λ$ ，按需对 $U$ 清零特征值太小的行与列，得到降到 $k$ 维的变换矩阵 $U_{k}$ （在某个方向的方差较小便排除这个维度，点云向维度平面投影降维）
对原始数据进行降维变换 $y_{i} = U_{k} x_{i}$ 得到降维数据

线性判别分析/广义判别分析

线性判别分析LDA原理及推导过程（非常详细） - 知乎
LDA的思想是：最大化类间均值距离，最小化类内方差。意思就是将数据投影在低维度上，并且投影后同种类别数据的投影点尽可能的接近，不同类别数据的投影点的中心点尽可能的远。

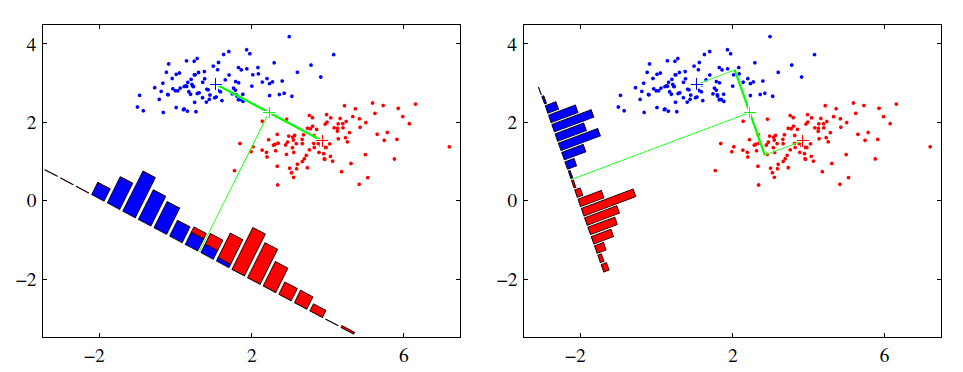
右图要比左图的投影效果好，因为右图的黑色数据和蓝色数据各个较为集中，且类别之间的距离明显。不过看图，和PCA不同，方差小的轴作为了横轴而不是纵轴。

有别于线性判别分析LDA，广义判别分析GDA使用了核函数方法，处理非线性判别问题。

缺失值比率

计算变量含有缺失值的比例，当缺失率很大时，那么认为，这个变量所携带的信息比较少。
不过是否删除，需要根据具体情况而定。如：缺失值同时表示没有或未知，而不含缺失值的部分和目标变量的相关性又很大。

因子分析

研究多个变量之间的内在联系，既隐变量，通过线性方法，将这些有内在联系的变量组合为新的变量，从而起到降维的效果。

步骤如下：

对数据进行标准化处理。
判断数据是否适合因子分析：KMO 和Bartlett 检验。
选择因子个数，针对特定研究会有主观的选择个数，也可以根据特征根判断，进行个数选择。
因子旋转。
转变为新变量。

独立成分分析

(3 封私信) 独立成分分析（Independent Component Analysis） - 知乎

以上提到的12种降维方法外，还有许多其他的方法，如：核PCA、小波变换等等。

神经网络池化

一文彻底搞懂CNN - 卷积和池化（Convolution And Pooling）卷积池化-CSDN博客
池化操作有多种方式，其中最常见的是最大值池化（Max Pooling）和平均池化（Average Pooling）。它们分别通过选取局部区域内的最大值和平均值来减少特征图的尺寸。
Pasted image 20250622165134.png
其实就是数据分块/抽样：减小特征图的维度来减少计算量和参数数量，同时还可以防止过拟合。

神经网络扁平化

CNN卷积神经网络中数据“扁平化”及其代码实现的讨论 - 知乎
 卷积神经网络中的池化与扁平化的概念-网易伏羲

扁平化操作将一个多维的特征图（张量）展开成为一个一维向量，以便将其作为输入传递给全连接层。后续的分类可以继续交给全连接层。

前向特征选择

选择一个特征，用每个特征训练模型，得到n个模型。
选择模型性能最佳的变量作为初始变量。
每次添加一个变量继续训练，重复上一过程，最后保留性能提升最大的变量。
一直添加，一直筛选，直到模型性能不再有明显提高。

反向特征消除

先获取数据集中的全部n个变量，然后用它们训练一个模型。
计算模型的性能。
在删除一个变量后计算模型的性能（剩余几个变量循环几次），即我们每次都去掉一个变量，用剩余的n-1个变量训练模型。
确定对模型性能影响最小的变量，把它删除。
重复此过程，直到不再能删除任何变量。

基于丢弃的方法

低方差过滤

基于权重的方法

层次分析法相对赋权

变异系数法

熵权法

灰关联系数赋权

灰关联系数

步骤

TOPSIS

数据包络分析

基于投影的方法

主成分分析

线性判别分析/广义判别分析

高相关性过滤

缺失值比率

因子分析

独立成分分析

神经网络池化

神经网络扁平化

前向特征选择

反向特征消除

基于过程的性能指标

积分型（拉格朗日型）性能指标

末值型（麦耶尔型）性能指标

复合型（波尔扎型）性能指标