Summary

静态数据的固有性质分析

协方差矩阵

如何直观地理解「协方差矩阵」？
刚体（1）：惯量张量 - 知乎
 PowerPoint Presentation
转动惯量的任意轴定理 - 豆丁网
 二次型与特征向量 - Bill_H - 博客园
 【数学】方差、协方差、协方差矩阵 - LENMOD - 博客园
 (52 封私信 / 80 条消息) 协方差矩阵的特征值与特征向量的几何意义 - 知乎

协方差

σ (x, y) = \frac{1}{n - 1} \sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})

多维数据的协方差矩阵

Σ = [\begin{array}{ccc} σ (x_{1}, x_{1}) & \dots & σ (x_{1}, x_{d}) \\ ⋮ & ⋱ & ⋮ \\ σ (x_{d}, x_{1}) & \dots & σ (x_{d}, x_{d}) \end{array}] \in R^{d \times d}

Question

先决证明：转动惯量的任意轴定理→方差的任意轴定理

与转动惯量区别：转动惯量是关于直线的平方和，方差是关于平面的平方和。
可以证明，存在“方差的任意轴定理”，于是

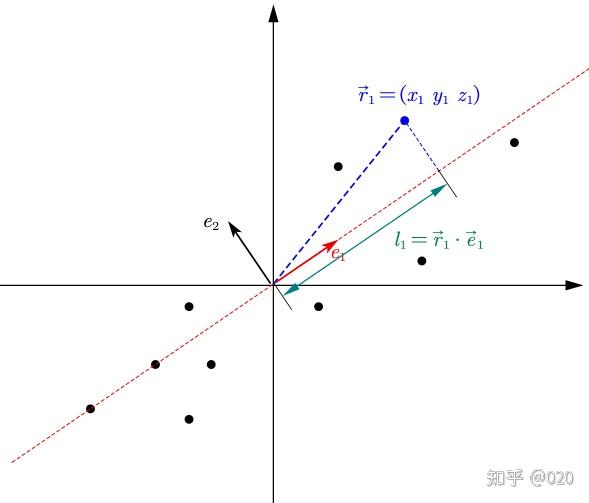
对于任意法向量的方差，其值与法向量构成一个二次型图形（如椭球面）。
对于某个法向量的单位矢量 $\vec{e}$ 和该方向的坐标 $q$ ，方差 $σ (q, q) = e^{T} Σ e$
对于方差的极值，就是协方差矩阵的特征值，对应法向量为协方差矩阵的特征向量，对应二次型图形的轴线（如椭球面的对称轴）。

如图，二维数据的协方差矩阵的特征值与特征向量

信息熵

处暑 | 从热力学与统计物理到信息论编码——浅谈“熵” - 智源社区
 从热力学熵到香农熵、交叉熵和KL Divergence（1）：从热力学说起 - 知乎
 从热力学熵到香农熵、交叉熵和KL散度（2）：信息与信息熵 - 知乎

玻尔兹曼熵

从玻尔兹曼熵说起

S = k \log W

其中 $W$ 是微观状态的所有可能数， $k$ 是玻尔兹曼常数。在如下的物理模型中，假设粒子只有两种状态H和T，那么宏观状态有三种，微观状态有四种

直觉中的信息熵

在信息领域，熵经常被错误地等同于信息，熵是指“缺失的信息”，是在给定宏观状态下，要了解微观状态所需要问的Yes/No的问题数量的期望值。这个定义与香农熵紧密相关

我们通过一个例子来讨论信息量的度量问题：有两台字符发生器，按下表的概率分布随机产生A，B，C和D 4个字符。

	A	B	C	D
机器1	25%	25%	25%	25%
机器2	50%	25%	12.5%	12.5%

问：哪一台机器是产生的信息量更多？

我们按照香农的思路来重新组织一下这个问题：要猜出下一个字符，如果可以问机器问题，对于每台机器，平均所要问几个Yes/No问题？

显然，对于机器1，要问2个问题才能搞清楚下一个字符是什么。

$E = 2 \times \frac{1}{4} \times 4$

对于机器2，由于其50%的可能产生字符A，能否调整一下问法，尽量降低所需问题数量的期望值呢？

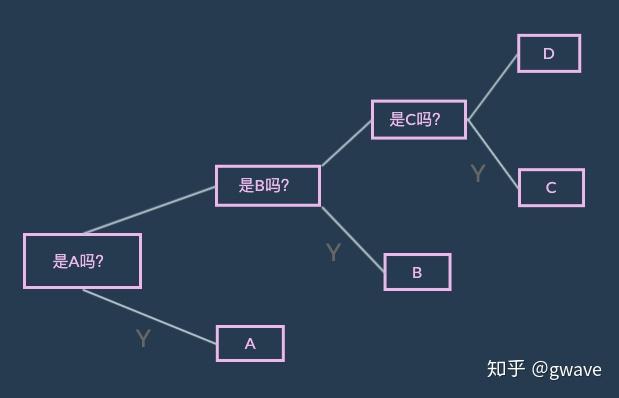
对于机器2，问题数的期望值为:

E [Q u e s t i o n s] = 0.5 \times 1 + 0.25 \times 2 + 0.125 \times 3 + 0.125 \times 3 = 1.75

如果要猜100个字符，对于机器1，要问200个问题；对于机器2，平均只需问175个问题
因为机器2的不确定性要小于机器1，也意味着机器1所产生的信息量大于机器2
每产生1个字符，机器1蕴含着2比特的信息，机器2只有1.75比特。
香农称这种不确定性的期望值的度量为“熵”，以字母H来表示，度量熵的单位是比特，相当于一次公平的投硬币所含的信息。

香农熵

香农熵公式推导与理解 | Bear's dream
我们再看这个问题期望的计算过程。

E [Q u e s t i o n s] = {0.5}^{1} \times 1 + {0.5}^{2} \times 2 + {0.5}^{3} \times 3 + {0.5}^{3} \times 3 = 1.75

可能读到这里会有疑问，这里的0.5、0.25、0.125都是题设规定的概率，如果换了题目的概率还适用吗？
先想想，换了题目的概率，你怎么确定，“确定子事件需要的问题数量”是1、2、3呢？
香农熵公式有一个结论

n u m b e r_o f_Y N_q u e s t i o n s = l o g_{2} (\frac{1}{p_{i}})

粗浅理解：机器能均等概率产生4种字符，则要2个问题，8种字符要3个问题，8是2的3次方，那么均等概率产生26种字符需要 $\log_{2} 26$ 个，大约4.7个问题吧。
再次理解：number of Y/N questions 取决于该outcome在问题树中的深度。概率越小的outcome，在问题树中的深度越深，所需的问题也越多，即所需问题数和发生概率成log反比关系。
证明：？？？
完整表述：
如果一个系统的n个事件具有彼此独立的概率 $p_{i} (i = 1, 2, \dots, n)$ ，那么存在一个独特的函数$$\begin{align}f(p_1,p_2,\cdots,p_n)=-C\sum_i^np_i\ln p_i\tag{9}\end{align}$$对于一组给定的约束，当函数 $f$ 取最大值时， $p_{i} (i = 1, 2, \dots, n)$ 是系统的最概然分布。

所以，香农熵的定义浮现：

H = \sum_{i = 1}^{n} p_{i} l o g_{2} (\frac{1}{p_{i}}) = - \sum_{i = 1}^{n} p_{i} l o g_{2} (p_{i})

还有吉布斯熵，在此基础上乘了玻尔兹曼常数

S = - k \sum_{i} p_{i} \ln p_{i}

还有一个有趣的定义

信 息 = k \sum_{i} p_{i} \ln p_{i}

信息也叫做负熵。

Note

感觉熵值大，带给我们的是一种“欲知后事如何”的兴奋，熵值小才是信息传达确定。这无关信息的好坏，有时候确定的信息让人昏睡，不确定的信息催人奋进，有时相反。

信息熵的性质

熵的性质：可加性和强可加性_熵的可加性-CSDN博客

KL散度

KL散度、JS散度、Wasserstein距离 - 范仁义 - 博客园

核方法

核方法、核技巧和核函数 - 知乎