关于噪点,序列信号的滤波平滑。FIR、IIR、维纳滤波、贝叶斯滤波、卡尔曼滤波、粒子滤波
突然想到,贝叶斯滤波,从概率的角度考虑,这不就是量子力学波函数的考虑吗
graph LR w((Observed)) --> F[Filter] --> e((Estimated))
1. 滤波(Filtering)——活在当下:利用当前和过去的数据,估计当前状态。
2. 预测(Prediction)——展望未来:基于当前和过去的数据,推测未来状态。
3. 平滑(Smoothing)——复盘过去:利用全部数据,优化全部状态的估计。

对,但不完整。滤波是在线调用的元件(信号变换器),预测是在线调用的元件(信号发生器)
平滑是离线调用的静态方法,但实际调用时候,我们往往是拿着一个元件(滤波器)对着波形发生作用,除非这个平滑方法不是按时间移动进行的,而是整体变换。
有限冲激响应滤波器FIR
如何通俗易懂地理解FIR/IIR滤波器? - 知乎
【模型预测控制】FIR模型 - 知乎
有限冲激响应:响应不是随着时间的推移无限趋近于0,而是在某个时间后就变成了0,也就是对于巴掌这个“冲激”的响应是“有限的”
将含噪声信号与低通滤波器的傅里叶逆变换值进行卷积,这个过程就是FIR滤波。我用一张图表示他们之间的关系:
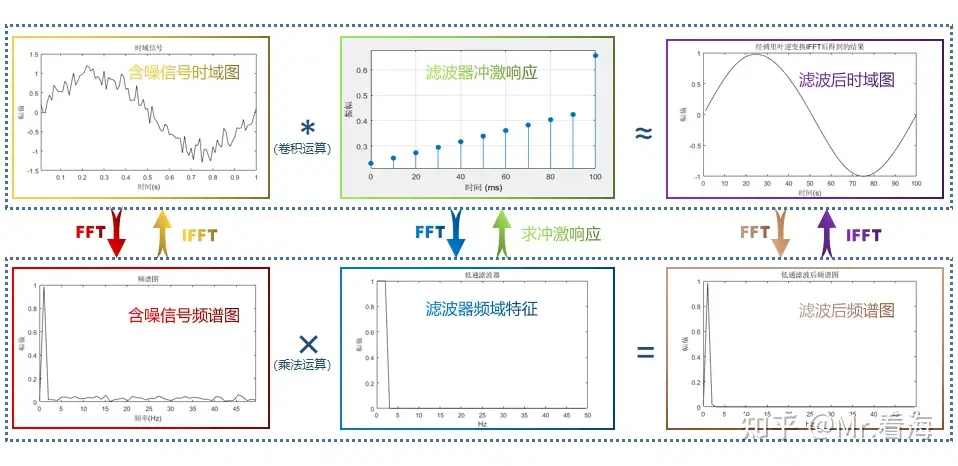
浓缩成一个表达式,表示FIR滤波器(直接型结构):
x代表待滤波数据,y代表输出数据;系数a0、a1、a2...就是滤波器的冲激响应系数。所以在FIR滤波器中,每一时刻的输出取决于之前的有限个输入,因此就是“有限冲激响应”。
写成Z变换传递函数的形式,可以看到分母全是1而分子全是z
所以这个传递函数只有零点,整个FIR滤波器也属于全零点系统
加权滑动平均
时间序列预测基本方法--移动平均(SMA、EMA、WMA) - 知乎
加权移动平均法 - MBA智库百科
使用卷积计算移动平均值 - XXX已失联 - 博客园
使用Numpy.convolve进行加权移动平均|极客笔记
下面的方法,所谓“预测方法”,其实只是预测前的预处理,平滑方法!别被误导了!
下图可以理解为这3个值分别乘以权重系数1/3再求和,那么上述滤波过程可以用下边这张动图来演示,应该是比较直观的了:

看到这里大家想到什么了吗。是的——是卷积。我们只需要知道:FIR滤波就是在时域上卷积的过程。卷积有一个重要性质:时域的卷积等于频域相乘。
只是平滑出的序列会比原序列多一两个时间点,于是就有了预测的功能。
如果进行这个预处理过程(由原始序列输出平滑序列,输出不会干扰输入),这是把原始波形放入FIR滤波器中再
如果继续往后预测(把输出作为输入自行迭代),放在预测模型中,这是不考虑白噪声的AR自回归模型
前提假设条件:序列相对平稳,没有趋势、季节性的情况。
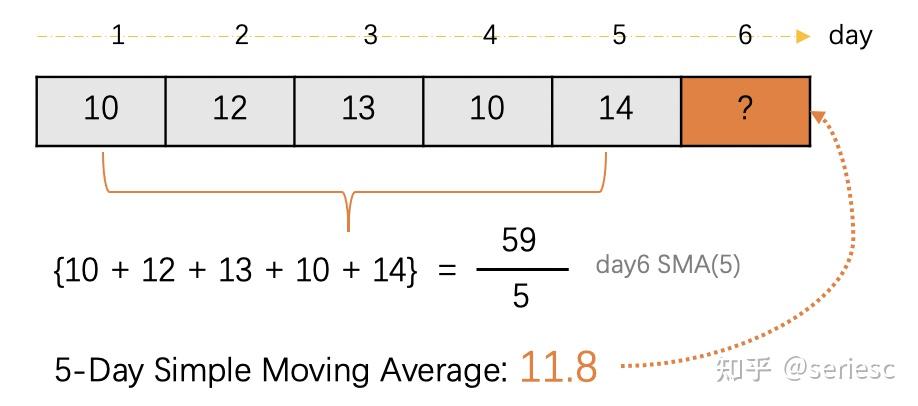
先说简单的移动平均。小儿科,直接上公式
n为窗口大小,
再说加权的移动平均。 n为窗口大小,
指数移动平均,就是加权移动平均的特殊形式罢了,给权重赋予指数规律(等比规律),冲激响应曲线是指数曲线
都是卷积模块罢了。卷积模块的输入输出,经过不同的接驳方式,可以得到信号发生器、滤波器,或者仅仅是平滑工具。
权重的整定:自适应滤波法
时间序列模型 (四):差分指数平滑法、 自适应滤波法_指数平滑滤波-CSDN博客
FIR的系统结构
数字信号处理—数字滤波器的各种系统结构 - 知乎
【数字信号处理】第五章 时域离散系统的网络结构 - 哔哩哔哩
说的就是信号流图可以化简成各种各样
无限冲激响应滤波器IIR
FIR是从滑动平均方法牵引出来的基于卷积的一种滤波方法,可以说FIR天然是具有直观的“数字处理”的特性的;
而今天讲到的IIR方法是和物理世界的模拟电路有着对应的联系,或者说它是对“模拟滤波器”的数字表达。
目前IIR数字滤波器设计的最通用方法是借助于模拟滤波器的设计方法——先设计一个合适的模拟滤波器(模拟原型滤波器),然后利用复值映射把模拟滤波器变换成数字滤波器。
无限冲激响应:如下图中的电路,在IN的位置给一个电压值后,电容会被充电,当IN的电压取消后(此时相当于给IN处加了一个冲激信号),电容的电量会被逐渐放掉,但是理论上永远不会变成0,所以输入信号会在后续无限长的时间内产生影响,也就是“无限冲激响应”。
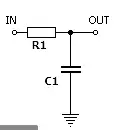
用一个公式概括IIR滤波器(直接型结构):
x代表待滤波数据,y代表输出数据;将输入信号的值乘以“a”系数(仍然是冲激响应系数),将先前从输出信号计算的值乘以“b”系数,并将乘积相加,可以找到输出信号中的每个点,上式称为递归公式。
由于本步骤的输出会作为下一步骤的输入,无限递归下去,所以一个时刻的影响就是无限的,也就是“无限冲激响应”。
先看这样的传递函数,可以看到分子全是1而分母全是z
所以这个传递函数只有极点,不包含x部分的IIR滤波器属于全极点系统
写成Z变换传递函数形式,可以看到一般的IIR既有零点又有极点,属于零极点系统
IIR的系统结构
数字信号处理—数字滤波器的各种系统结构 - 知乎
【数字信号处理】第五章 时域离散系统的网络结构 - 哔哩哔哩
说的就是信号流图可以化简成各种各样
模拟原型滤波器
巴特沃斯滤波器
切比雪夫滤波器
贝塞尔滤波器
椭圆滤波器
维纳滤波
信号处理--维纳滤波(wiener filter) - 知乎
维纳滤波 Wiener Filter - 知乎
3-线性估计与正交性原理 - 知乎
正交性原理与维纳霍夫(正则)方程-CSDN博客
维纳滤波——Wiener Filter(一些理解)
捷联惯导系统学习5.1(贝叶斯估计、维纳滤波)贝叶斯与维纳滤波-CSDN博客
维纳滤波是一种线性最小均方误差(LMMSE)估计。(权重与概率无关,与时间先后有关)
观测精确量
估计量:
残差
我们要得到让方差最小的估计量。也可以通过求偏导求解,但反正 有一个正交性原理,即最优滤波时残差与输入不相关。
尝试直接化:
求和换序:
识别自相关函数:
这是什么鬼?看来不能直接求。或许要结合正交性原理
老老实实求偏导写出维纳霍夫积分方程,毕竟它要求偏导为零才成立。
记方差为
设偏导为零得维纳霍夫积分方程
在频域有(P是功率谱,信号功率在频域的分布状况)
什么是功率谱?
其中 , 进而传递函数
维纳滤波的离散形式,或许和卷积变换的矩阵形式有异曲同工之妙?
贝叶斯滤波
#贝叶斯滤波 #概率状态空间模型 #贝叶斯估计
滤波估计理论(一)——贝叶斯滤波_bayesian filtering and smoothing-CSDN博客
从概率到贝叶斯滤波 - 知乎
其实是把一个其他来源的估计量,和当前来源的实测量,用期望(均值)进行融合。
如果:估计方法就是加权移动平均法而不是基于概率或其他传感器,估计值的来源就是原始波形的加权平均;直接和原始波形的当前值用均值进行融合——就会退化成FIR滤波器。
因此贝叶斯滤波的根本不同就是把概率分布引入了滤波器理论中。
符号运算顺序:(a,b,c)|(d,e,f),先算逗号“与”,再算竖线“在该情况下”
拿出一个概率状态空间模型(经过马尔可夫链简化)。
于是,状态空间模型的方程可以写为
其中,Q为过程噪声,R为观测噪声,都服从自己的概率分布。
于是我们的已知量可以表示为
即噪声服从的概率密度函数平移
贝叶斯滤波,本质上是递归的贝叶斯估计的求解前奏(前面都是对概率分布的更新,也就最后一步是在估计)。
单步预测
预测出先验分布
(离散形式便是马尔可夫链中经典的CK方程)
可以用
量测更新
修正成后验分布
可以用
后验估计
对x的估计,即为贝叶斯估计的最后一步,对后验概率求期望。当然,也可以用其他估计,如最大后验概率估计、最大似然估计……
循环往复,周而复始。

卡尔曼滤波
(49 封私信 / 80 条消息) 从贝叶斯滤波到卡尔曼滤波 - 知乎
(49 封私信 / 80 条消息) 深入浅出理解卡尔曼滤波【实例、公式、代码和图】 - 知乎
假设:
状态转移函数为线性函数
观测函数为线性函数
假设:
状态量服从正态分布
观测量服从正态分布
过程噪声服从均值为0的正态分布
观测噪声服从均值为0的正态分布
单步预测

量测更新
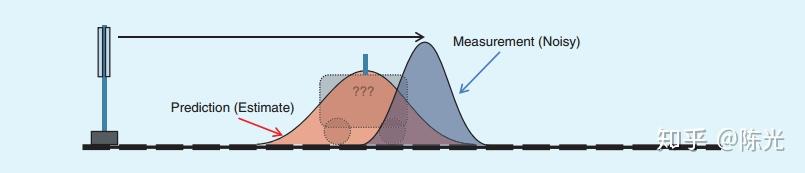
加权输出

粒子滤波
#序列重要性采样
从贝叶斯滤波到粒子滤波 - 知乎
粒子滤波到底是怎么得到的? - 知乎
贝叶斯滤波到粒子滤波的理解_粒子滤波比 贝叶斯推断的区别-CSDN博客(他是不是搞错了,拿先验分布作为建议分布,是无法得出简洁的权重更新公式的)
particle filtering---粒子滤波(讲的很通俗易懂)-CSDN博客
Particle_filter 粒子滤波器 的学习笔记 - 小胖蛋 - 博客园
定位算法 -- MCL蒙特卡洛(粒子)滤波 - 知乎
slam 学习之 AMCL 概念与原理分析_amcl定位原理-CSDN博客
AMCL 原理解读 - Gaowaly - 博客园
第十一课 粒子滤波与蒙特卡洛定位简介 - 知乎
粒子滤波详解【3/3】:增强蒙特卡洛定位AMCL
采样方法
粒子滤波中,(最优的建议分布无疑就是真实的后验分布本身,但是后验分布难以积分求出)建议分布同样需要我们自己设计。
建议分布的设计已经发展出很多形式,并由此衍生出种类繁多的粒子滤波变种:
- 以 UKF 生成建议分布的无迹粒子滤波(Unscented Particle Filter,UPF)
- 以 EKF 生成建议分布的扩展卡尔曼粒子滤波(Extended Kalman Particle Filter,EKPF)
- 通过构建辅助变量,提升和观测更为匹配的粒子被采样的概率的辅助粒子滤波(Auxiliary Particle Filter,APF)
我们通常选择这个“先验状态转移概率分布”,这是后话
无论选择什么分布,接下来的推导基于一个假设的递推关系
若我们只关心当前
单步采样
通过
用建议粒子群来表示先验分布,而不是用积分求出的函数来表示
采样规则如下
序列采样中,新一轮的粒子群可以基于上一轮的基础再进行迁移,所以我并没有写
当然时间久了,随着“权重更新”的进行,粒子的权重质量会越来越集中(粒子退化),所以会引入“重采样”步骤,把权重大的粒子“裂解”成多个小粒子
常用的重采样方法:多项式重采样、分层重采样、系统重采样、残差重采样
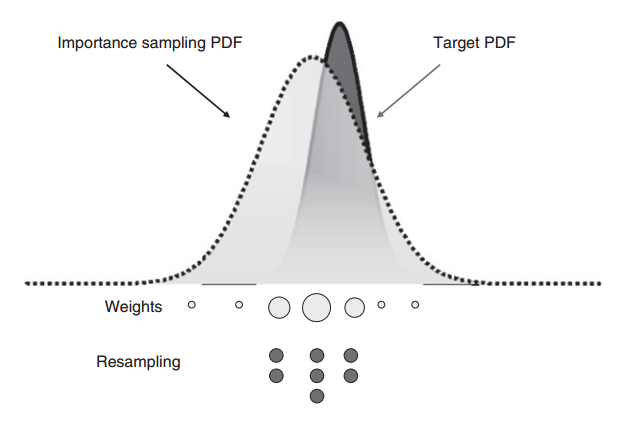
当然,如果权重过于集中,“裂解”的小粒子也只会是大粒子的复制体,多样性丧失(样本贫化)
样本贫化极有可能导致滤波器发散,为了处理样本贫化问题,已经发展出很多方法,例如正则粒子滤波(Regularized Particle Filter,RPF)
权重更新
通过
用加权粒子群来表示后验分布,而不是用积分求出的函数来表示
这里只能用
因为权重的递推,是基于
选取状态转移分布作为建议分布采样,可以用作SIR滤波器
记得权重归一化哦
粒子估计
对加权粒子群求均值,得到期望,代替后验估计
通过加权粒子群的求和平均来表示期望,而不是用积分求出的值来表示
输出估计
状态估计
AMCL深入解析 3/4 - 解决的核心问题 - 知乎
基于SIR滤波的定位算法称为蒙特卡洛定位(Monte Carlo Localization,MCL)
在机器人定位问题中(激光雷达为例),状态量是机器人的位姿,观测量是激光雷达测得的各个角度的点云距离(波束模型)。状态量结合地图可以换算得出估计量,粒子滤波就是让估计波束“跟随”观测波束
从最优化的角度思考,这不就是一种点云匹配的算法吗?不就是最优化的目标频繁变化吗?
AMCL算法相比MCL算法,在机器人遭到绑架的时候,会随机注入粒子(injection of random particles)
(49 封私信 / 80 条消息) 卡尔曼滤波、粒子滤波、贝叶斯理论、最优化介绍 - 知乎
科普一下ROS中的AMCL算法_amcl particle swarm-CSDN博客
对ICP、PL-ICP、NICP、IMLS-ICP匹配算法的解析-CSDN博客
【定位】纯激光导航定位丢失/漂移问题的优化方案及思考_amcl定位精度低怎么办-CSDN博客
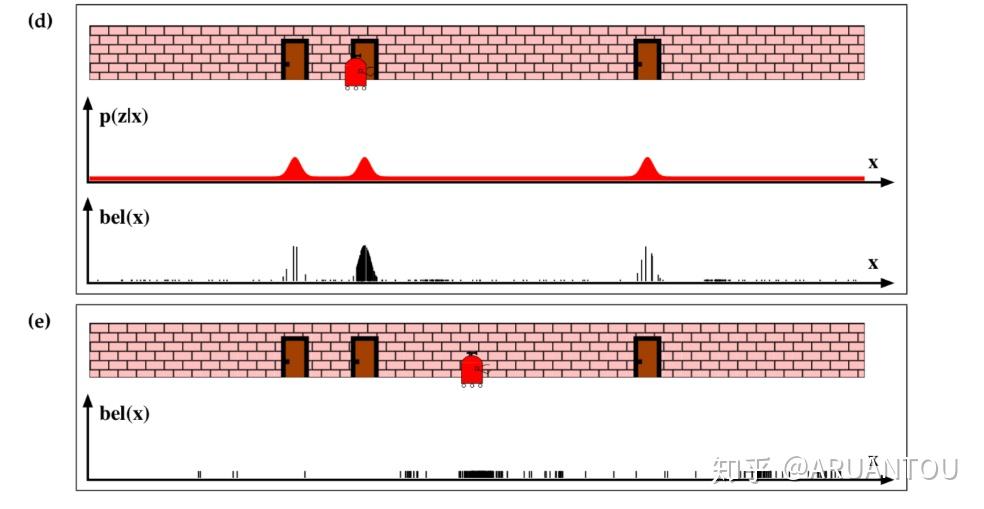
通过一个实例来感觉下(下面“权重更新”看来是定位的关键,而“权重更新”的关键又是观测分布
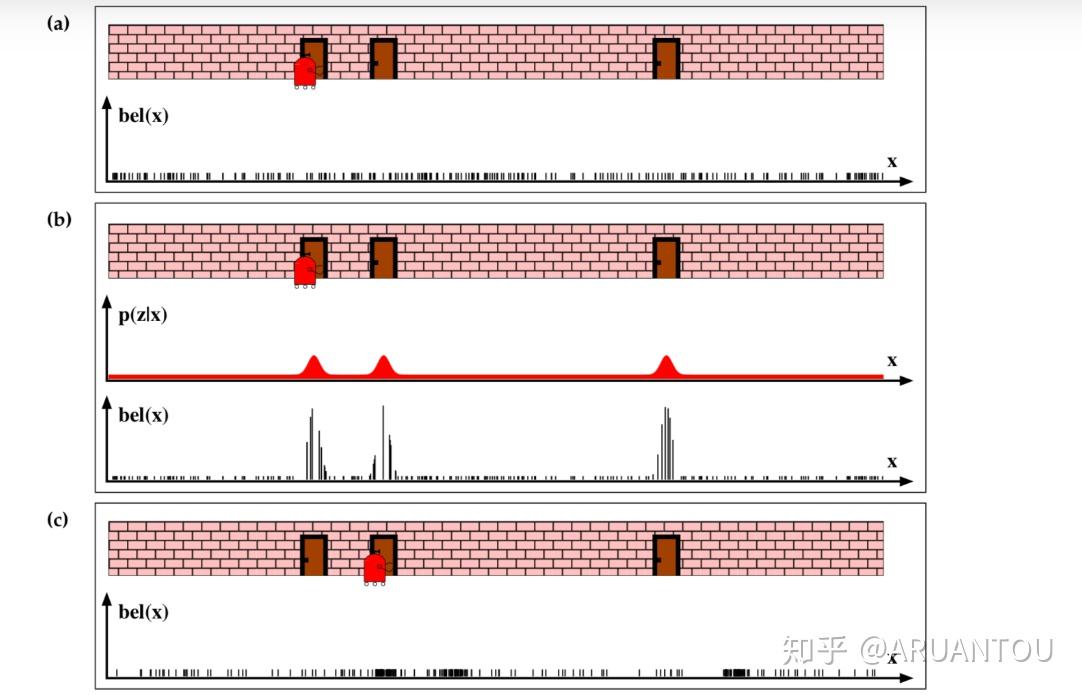
a)图, 我们看到机器人初始在一个门的位置,但是这时候机器人并不知道它自己在哪,这时候我们初始化所有的粒子,并且所有粒子的权重都是一样的。
b)图,这时候机器人通过传感器得知面前是一个门,这时候可以看到和门比较近的粒子的权重都提高了。
c)图,进行重采样之后,机器人移动后,我们可以看到采样后的粒子都集中在原来靠近门的这些粒子点。就是图中黑色密集的位置。
继续看D)图,这时候机器人重新感知,得知面前还是一个门,这时候,原来采样的靠近门的粒子权重变大。从图中已经看到主要的采样点已经集中在第二个门的位置了,机器人现在就知道自己的位置是在第二个门了。
之后在e)图中,冲采样,再次移动机器人,就可以知道机器人这次移动到的位置在中间了。
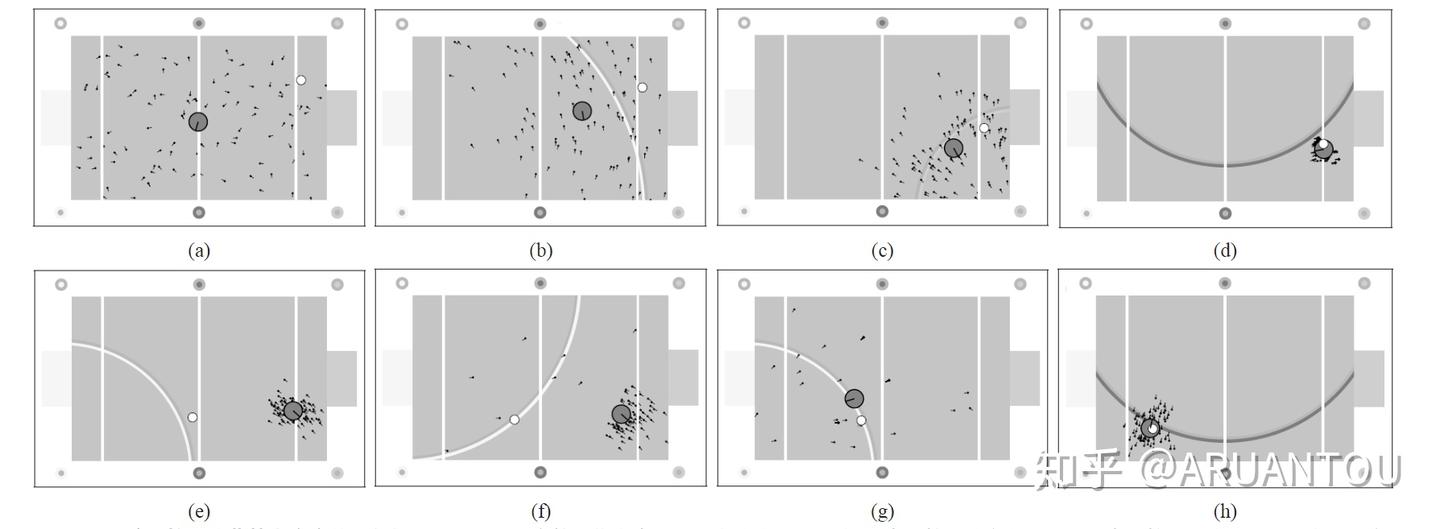
最后看下实例图,感受下粒子滤波的定位: