动态数据的固有性质分析
后向差分
通常会用倒三角(梯度算符)表示
卷积
离散卷积
如何通俗的理解z变换? - 知乎
如何通俗易懂地理解FIR/IIR滤波器? - 知乎
【离散系统的时域分析】3. 卷积和_竖乘法求卷积-CSDN博客
乘法的竖式运算与卷积→卷积的本质 - 简书
在信号与系统中,在计算卷积和用竖式相乘对位相加时,如何确定零点的位置_百度知道
离散信号卷积计算:竖式乘法与图表法 - CSDN文库
一、卷积运算的结果
二、多项式乘积的结果
三、设
四、滑动窗口的结果(如果按方括号翻转式就是直接对应,如果按圆括号原式则是对称对应)

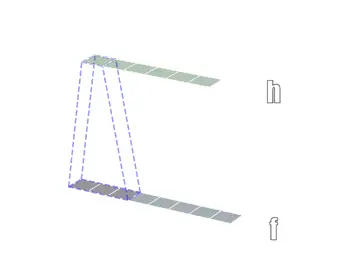
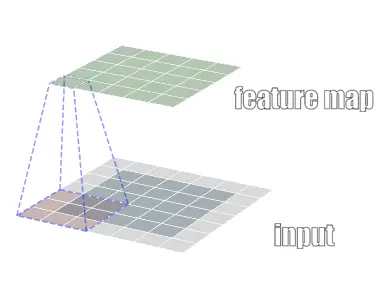
对于更高维的数据,从翻转变成了中心对称。
u(t)可以视为一个波形从左往右撞进了h(t),每一个时刻,都是最新的u(t)刚刚与h(0)相遇,最初的u(0)刚刚与h(t)相遇。
是否可以据此设计新的基于二进制数码卷积的乘法器电路?
让我们看二、三、四式和一式的关系。
三、四式,实际上是二式的具体计算过程
四式是对双边的排列组合(按数位求和)
三式是对单边的拆分组合(乘法分配律)
二式是大名鼎鼎的Z变换,为数位赋予了时间顺序的意义,把数列运算变成了多项式运算
比方说,第一秒你给怪上了毒,第二秒两个队友给怪叠加上了毒
中毒状态第一秒掉3点血,第二秒掉2点血,第三秒掉1点血
通过多项式乘法,同一时间节点一一对应,就计算出了总的中毒扣血序列
一式就是以上过程的简写,序列的卷积。如果不按二式的计算方法就是如下
如果冲激响应就是
连续卷积
现在拿出一个存在阻尼但是欠阻尼的弹簧系统。
设输入量为
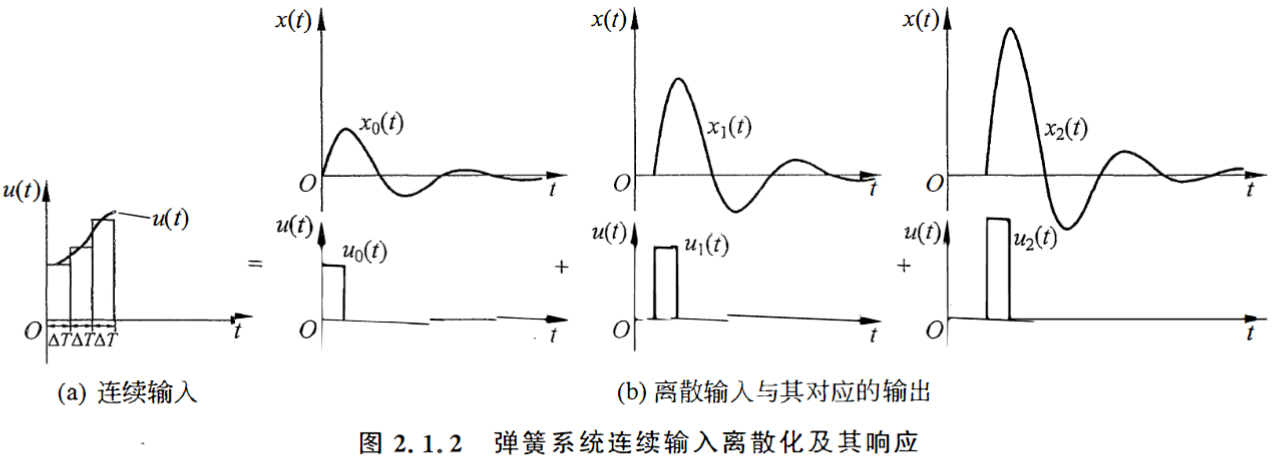
把连续受力分解为冲激元,以冲激元
而输出的波形也就是
输入冲激的累加,就是输入信号本身。
输出响应的累加,就是输出信号本身。
冲激响应,可能是振荡,可能是衰减,总之都是(t-τ)的函数h(t-τ)
微元地累加,这是个积分,卷积的定义,由此诞生。
如果冲激响应是
高数课本第四章里面好像出现过?我当时是画三维图解决的
一个函数h即可描述这个算子对信号的加工作用。知道了元件的h,我们就可以根据u来求出x
微分方程可以描述元件,卷积的核函数也可以描述元件。
求解输出的过程,可以是求解微分方程的过程,也可以是求解卷积运算的过程。
点积、正交,函数与向量的关系
用
可以理解为:函数是“维度连续的向量”,向量是“定义域离散的函数”
周期卷积
循环卷积
相关系数
能量
变换
傅里叶级数:周期函数的变换
从傅里叶级数到傅里叶变换 (From Fourier Series to Fourier transform)
FS,FT,DFS,DTFT,DFT,FFT的联系和区别 - 骏骏 - 博客园
在一定的条件 下,任何周期为 T 的函数 f(t) ,都可用一系列以 T 为周期的正弦函数所组成的级数来表示。由于(积化和差)
对应于向量的正交分解,这就是函数的正交分解。
正如向量正交分解出的坐标为向量在各个方向的投影,
傅里叶级数确定系数的方式也是求投影,系数就是投影得到的坐标。
对常函数
对
对
对于周期宽度不同的函数,替换掉系数π,也就是仿射变换即可。
代入系数得
其中设
这就是受频率影响的卷积
尝试用指数形式表示:
进一步,推广到复数域。我们知道
也就是说
则任何一个周期函数
若求
则上式右端积分中只有
对于三角函数系、虚指数函数系,从-l到l还是从0到2l,应该是没有影响(诱导公式)
离散傅里叶级数:周期数列的变换
离散信号(四)| 周期信号 |离散傅里叶级数(DFS)推导 + 主要性质(周期卷积定理、帕斯瓦尔定理)帕塞瓦尔定理 离散信号-CSDN博客
类似于傅里叶级数的复数形式,对于截取长度为N的数列,截取周期为N,对应的角频率为2π/N
注意,接下来的n其实不是角频率,
由于是离散量,角频率的范围不再是0到+∞,而是0到
周期为N的周期序列{a_n},其离散傅里叶级数为
其中,DFS的逆变换序列
离散信号,也没有周期到正无穷的说法,所以离散傅里叶变换的形式和离散傅里叶级数的形式一样
傅里叶变换:非周期函数的变换
(48 封私信 / 80 条消息) 傅里叶级数和傅里叶变换是什么关系? - 知乎
傅里叶变换将周期推广到无穷,能对具有任意长度的信号做展开。
对于非周期函数,先裁剪到
而
在
尝试用指数形式表示
拆分
后半段变换积分区间(令ω=-ω)
结果
类似傅里叶级数的复数形式(或许是出于对称性),傅里叶变换便是这么定义的:
可以看到,无非是把
拉普拉斯变换:非周期发散函数手动收敛
本身就是针对积分发散的函数来的,那假如对周期函数来这一出,那周期函数也不周期了,何苦呢,所以没有“拉普拉斯级数”
(48 封私信 / 80 条消息) 一个信号存在傅里叶变换就一定存在拉普拉斯变换吗? - 知乎
对信号
两边同乘
拉普拉斯变换和其逆变换一目了然。这其实体现了指数衰减函数在傅里叶变换里面一个“自由穿行”的特性(微分算子的移位法则!),我既可以参与τ的积分,也可以出来作为ω的参数
拉普拉斯逆变换,是先对已衰减结果进行傅里叶逆变换,再除去指数衰减函数的过程,压缩——变换——逆变换——解压,正是因为
拉普拉斯变换是附带预处理衰减的傅里叶变换,傅里叶变换是拉普拉斯变换的不做衰减的特殊形式
奇怪的东西
拉普拉斯级数 -- 来自 - 数学天地啥?这和信号与系统有关系吗?
信号的正交分解与广义傅里叶级数 - 知乎和拉普拉斯没啥关系
(48 封私信 / 80 条消息) 震惊!Laplace变换的本质竟然是…… - 知乎这只是对拉普拉斯变换后的频域函数进行展开罢了
离散时间傅里叶变换:非周期数列的变换
离散信号(六)| 非周期信号 | 离散时间傅里叶变换(DTFT)+ DTFT、DFS及CTFT之间的关系_dtfs和ctft和dtft和dtfs之间转换-CSDN博客
【信号与系统学习笔记】—— 离散时间非周期信号的傅里叶变换 (DTFT)【概念+性质 一站式全解析】-CSDN博客
(48 封私信 / 80 条消息) 离散时间傅里叶变换(DTFT)、离散傅里叶变换(DFT)和快速傅里叶变换(FFT)之间的联系和区别 - 知乎
FS,FT,DFS,DTFT,DFT,FFT的联系和区别 - 骏骏 - 博客园
DFT与DTFT区别是什么? - 知乎
DFT针对有限长信号,DTFT针对无限长信号。DTFT是N→∞时DFT的极限。
对离散傅里叶级数,让N趋近于正无穷
在连续傅里叶变换中,
要求内层从数列求和变成级数求和,
额外的充分条件:
结果(抄网上的,周期还是平移到对称的区间了)
离散时间拉普拉斯变换:非周期数列手动收敛,应该就是Z变换
或许可以把信号进行指数衰减后再进行DTFT,那就是离散时间拉普拉斯变换了。看看后面的推导,其实应该就是Z变换中,
连续Z变换,就是拉普拉斯变换:积分发散函数的变换
说一下连续 - 离散(s-z)系统的转换,和数值积分 - 知乎
s到z变换详解-CSDN博客
N5650_3.pdf
那么傅里叶变换和拉普拉斯变换,会不会是某种“连续的Z变换”呢?
猜想:
N5650_3.pdf
A generalization to the Fourier transform of a sequence is the z-transform. In the continuous-time the corresponding generalization is the Laplace transform.
啊……别猜了!看看拉普拉斯变换(单边)吧!
令
好吧,洗洗睡了
Z变换,就是离散拉普拉斯变换:求和发散数列的变换
如何通俗的理解z变换? - 知乎
信号与系统(7)——Z变换 - 知乎
[离散时间信号处理学习笔记] 8. z逆变换 - TaigaComplex - 博客园
频域信号分析基础-33 z逆变换 - 知乎
式中C表示的是收敛域内的一条闭合曲线:
得到Z变换及逆变换
双边变换:
单边变换:
由信号与系统(4)——离散时间傅里叶变换中讲解的DTFT的表达式:
可以得到Z变换与DTFT之间的关系,即
故DTFT是单位圆上的Z变换!!!
短时傅里叶变换
傅里叶变换、小波变换、拉普拉斯变换学习笔记 - 知乎
从傅里叶(Fourier)变换到伽柏(Gabor)变换再到小波(Wavelet)变换_gabor变换-CSDN博客
MATLAB信号处理(5)常见窗函数的使用 - 知乎
几种常见窗函数的特性 - 知乎
傅里叶变换中的不确定性原理(一) - 知乎
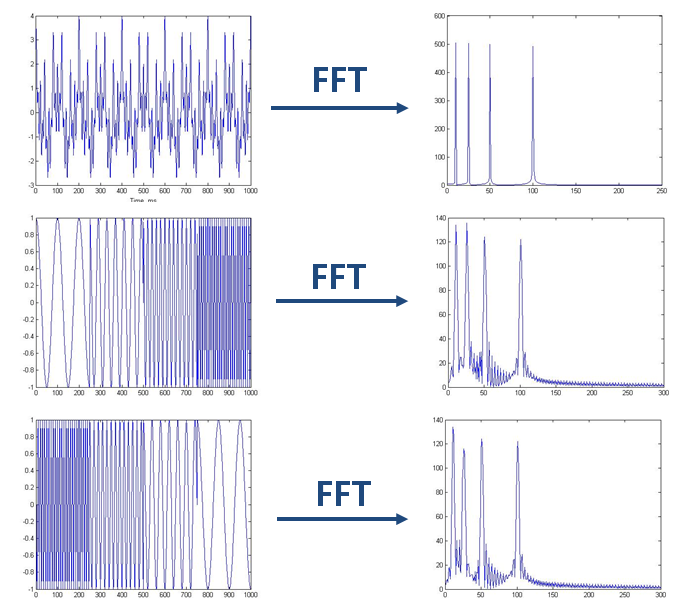
对于频率随着时间变化的非平稳信号,直接进行傅里叶变换容易丢失时域上的频率变化信息
拉普拉斯变换给信号手动乘上指数衰减,而短时傅里叶变换给信号手动乘上窗函数
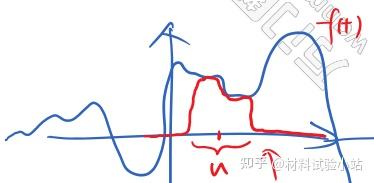
上图原始f(t)在窗函数作用下,只有红色窗函数部分起作用。
例如矩形窗的定义
可以取矩形窗、Hanning窗、Hamming窗、Gauss窗等等。一般把取Gauss窗函数的称为Gabor变换

定义基函数为
对于不同位置的窗口进行短时傅里叶变换,得到三维时频图。
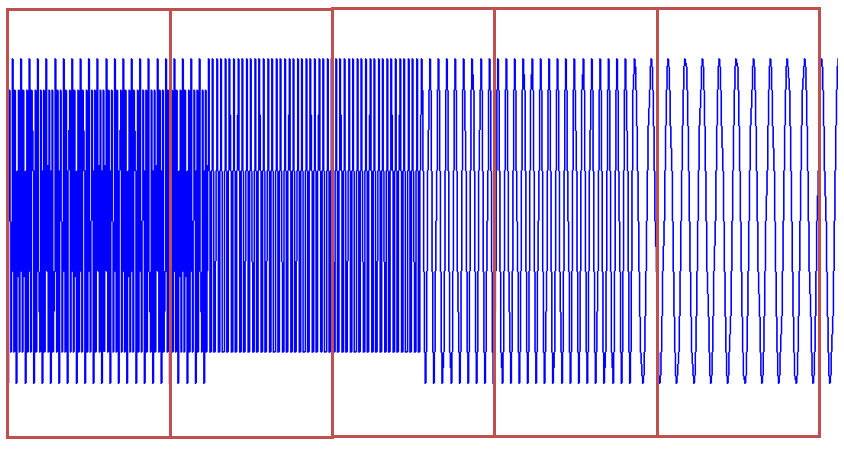
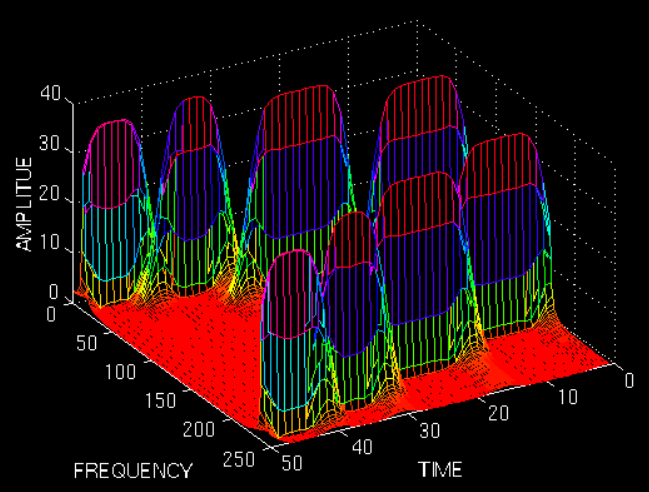
窗太窄,对频率的分辨差;窗太宽,对时间的分辨差

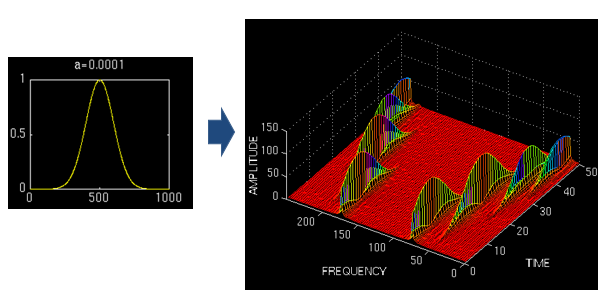
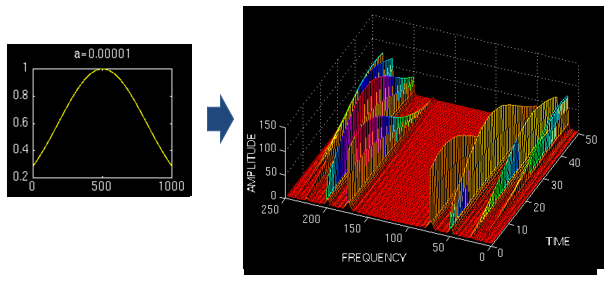
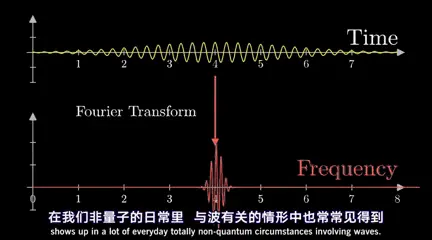
可以用海森堡不确定性原理来解释。类似于我们不能同时获取一个粒子的动量和位置,我们也不能同时获取信号绝对精准的时刻和频率。这也是一对不可兼得的矛盾体。我们不知道在某个瞬间哪个频率分量存在,我们知道的只能是在一个时间段内某个频带的分量存在。 所以绝对意义的瞬时频率是不存在的。
离散短时傅里叶变换
小波变换
The Wavelet Tutorial
形象易懂讲解算法I——小波变换 - 知乎
一文带你理解小波分析(附详细代码) - 知乎
小波分析——2. 小波函数及其逆函数_haar小波函数的公式-CSDN博客
- Gabor变换时频窗口的大小、形状不能随频率的变化而变化
- 因为信号的频率与周期成反比,对高频部分希望能给出相对较窄的时间窗口,以提高分辨率
- 在低频部分则希望能给出相对较宽的时间窗口,以保证信息的完整性
- Gabor变换基函数不能成为正交系,因此为了不丢失信息,在信号分析或数值计算时必须采用非正交的冗余基,这就增加了不必要的计算量和存储量。
什么是小波呢?所谓小波就是小的波形,“小”即具有衰减性,“波”是指具有波动性。
在说“小波(wavelet)”之前得先说“波(wave)”:
傅里叶变换就是基于这些“波”(正弦和余弦),它从负无穷到正无穷都存在,而小波变换则是基于以下的这种“小波”:
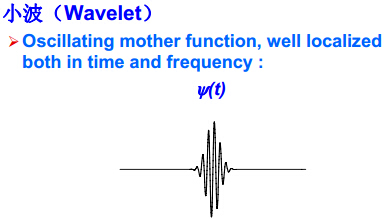
小波做的改变就在于,将无限长的三角函数基换成了有限长的会衰减的小波基。

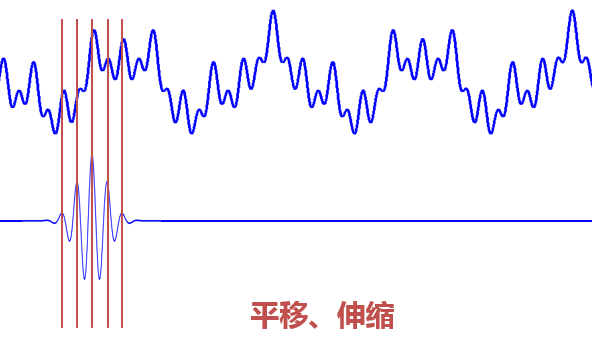
不同于傅里叶变换,变量只有频率ω,小波变换有两个变量:尺度a(scale)和平移量 τ(translation)。这也构成了三维时频图的水平方向两个坐标轴。真正的小波是基于小波母函数拉伸而来的:
ψ(t)是小波母函数(小波基函数),决定小波的形状。尺度a控制小波函数的伸缩,平移量 τ控制小波函数的平移。尺度就对应于频率(反比),平移量 τ就对应于时间。
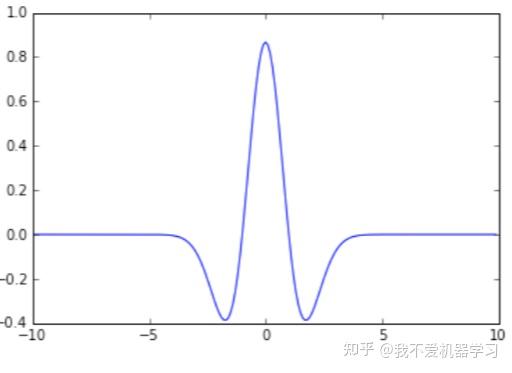
注意,小波函数满足正交条件;总的积分(也就是总的均值)必须为零。一个经典的小波是墨西哥帽子函数,是高斯函数(正态分布的概率分布函数)的重缩放负二阶导数
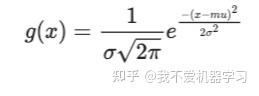
代入
小波变换同样有可逆的逆变换:
执行连续小波函数的逆运算,其实等价于小波函数与所得系数的连续卷积,即可以简要的表达为:
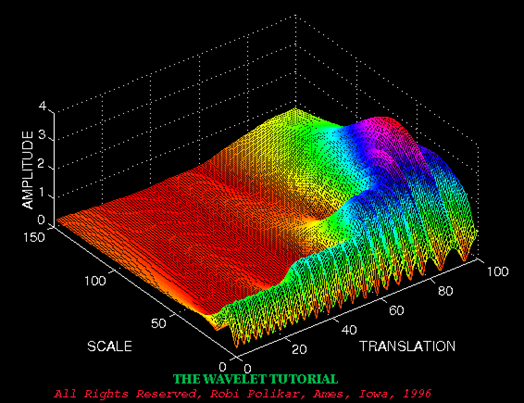
离散小波变换
离散小波变换(DWT)详解-CSDN博客
小波变换——公式整理和简单介绍 - 知乎
离散小波变换-数学百科
离散小波变换 🎯 - Eureka!
離散小波變換 - Wikiwand
算子、微分方程、差分方程
第五讲 信号流图 - 知乎
时间序列分析:延迟算子和差分算子 | nex3z's blog
【信号与系统】(二十三) z变换与z域分析——z变换及其性质-CSDN博客
差分方程到Z变换的转换 - 知乎
采样定理
时域的乘积变成频域的卷积
频域的卷积变成时域的乘积