关于给定目标点(作为参数),目标序列的生成。比例积分微分控制、最优控制、模型预测控制……
如果这个器件是开环的,那么应该就是一个插值器
graph LR C[Global Planner is Controller] --> e[(Effector Path)] --> m[/Graph or Map/] --> p((My Position)) p --> C
ROS中编写自己全局路径规划插件实现固定路线规划(1)ros全局路径规划-CSDN博客
move_base配置参数解析_node pkg = move base-CSDN博客
数学建模6——路径规划的各种算法(Dijkstra、Floyd、A*、D*、RRT*、LPA*)路径算法-CSDN博客
【规划】目录与总结_全局路径规划和局部路径规划-CSDN博客
如何设计局部规划器 - 知乎
ROS MoveBase与路径规划 - 数星星的猫 - 博客园
Bug
【机器人规划】Bug解析_bug1和bug2算法的优势场景-CSDN博客
人工势场法
【路径规划】局部路径规划算法——人工势场法(含python实现 | c++实现)人工势场法路径规划-CSDN博客
APF方法的local planner | zhangyuanes
不通过引力导向目标,而是寻找测地线,“测地线势场法”?
结合机器人的形状,发明“刚体人工势场法”,模拟刚体在钉板中的下落?
添加粘滞阻力,和路程损耗,PID势场法?
贪心算法
一句话,前向求解,但是非最优解全部被抛弃了。而动态规划保留了这些数据。
极大值原理(哈密顿函数法)
动态规划思想的基本原理
看一遍就理解:动态规划详解 - 知乎
动态规划算法的基本思想-求解步骤-基本要素和一些经典的动态规划问题【干货】-CSDN博客
戴克斯特拉算法(Dijkstra)的本质是贪心,还是动态规划? - 知乎
7.3 分治算法 | 算法通关手册(LeetCode)
8.1 动态规划基础 | 算法通关手册(LeetCode)
动态规划与静态规划、递归、分治、回溯 - 知乎
动态规划(dynamic programming,DP)和贪心算法(greedy algorithm,GA)的区别是什么? - 知乎
动态规划算法与分治法类似,其基本思想也是将待求解问题分解成若干个子问题。
对于独立子问题的分治法
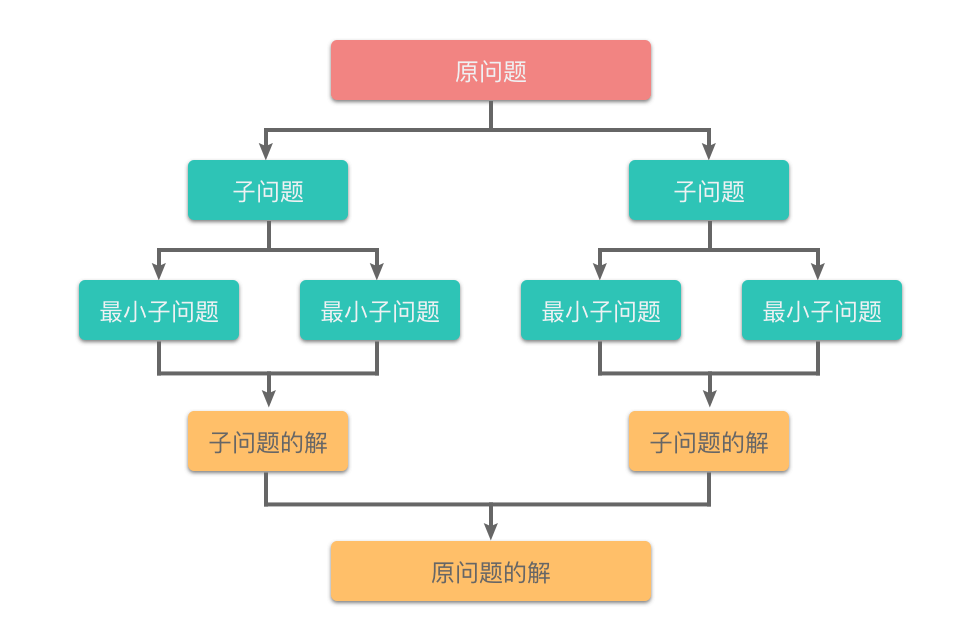
用分治法分解动态规划适用的问题,经分解得到的子问题往往不是互相独立的。不同子问题的数目常常只有多项式量级。在用分治法求解时,再套用递归减少代码量,有些子问题被重复计算了许多次。
★ leetcode原题:一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个 10 级的台阶总共有多少种跳法。
- 要想跳到第10级台阶,要么是先跳到第9级,然后再跳1级台阶上去;要么是先跳到第8级,然后一次迈2级台阶上去。
- 以此类推,即通用公式为: f(n) = f(n-1) + f(n-2)
但是画出如下递归树
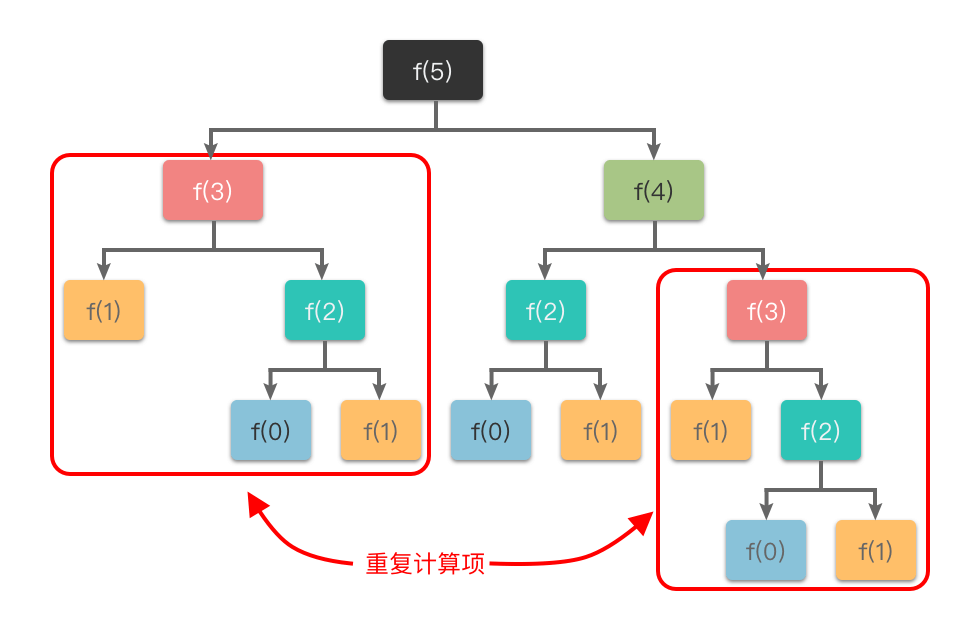
递归解法的时间复杂度 = O(1) * O(2^n) = O(2^n),重复计算严重!!
同理,在图最短路径问题中,经过同一小段局部路径的过程,都不知道会被重复走过多少遍呐!
如果能够保存已解决的子问题的答案,而在需要时再找出已求得的答案,就可以避免大量重复计算,从而得到多项式时间算法(指的是算法的时间复杂度)。
保存方案一:带备忘录的分治递归解法(自顶向下)
- 第一步,f(10)= f(9) + f(8),f(9) 和f(8)都需要计算出来,然后再加到备忘录中,如下:
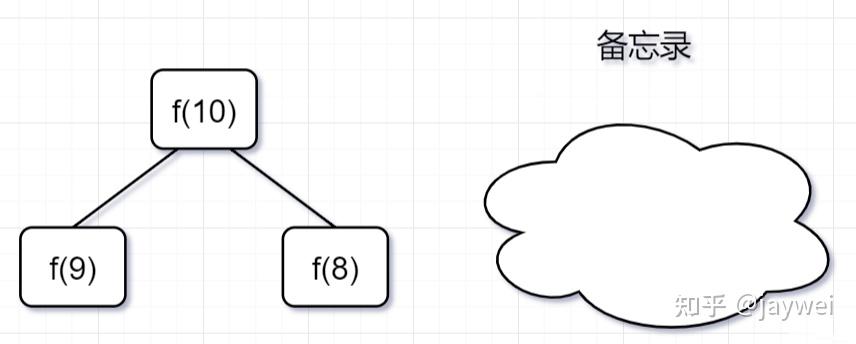
- 第二步, f(9) = f(8)+ f(7),f(8)= f(7)+ f(6), 因为 f(8) 已经在备忘录中啦,所以可以省掉,f(7),f(6)都需要计算出来,加到备忘录中~
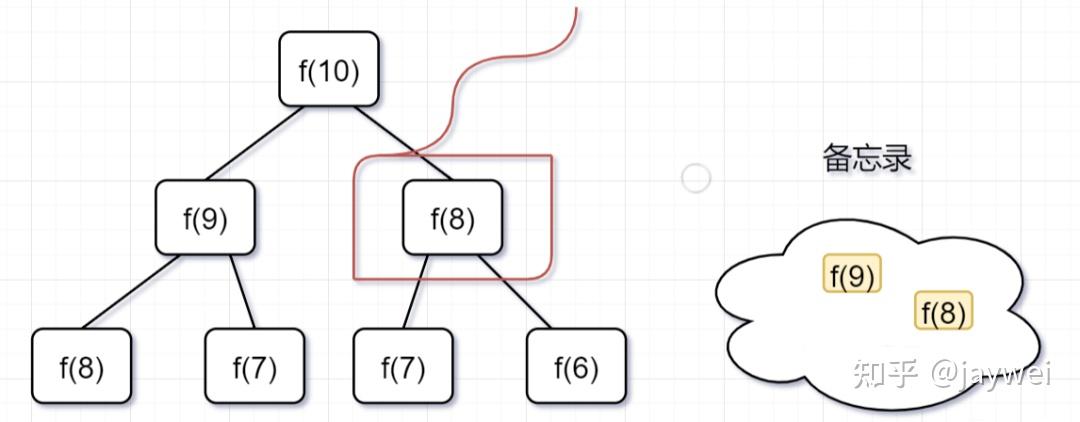
第三步, f(8) = f(7)+ f(6),发现f(8),f(7),f(6)全部都在备忘录上了,所以都可以剪掉。
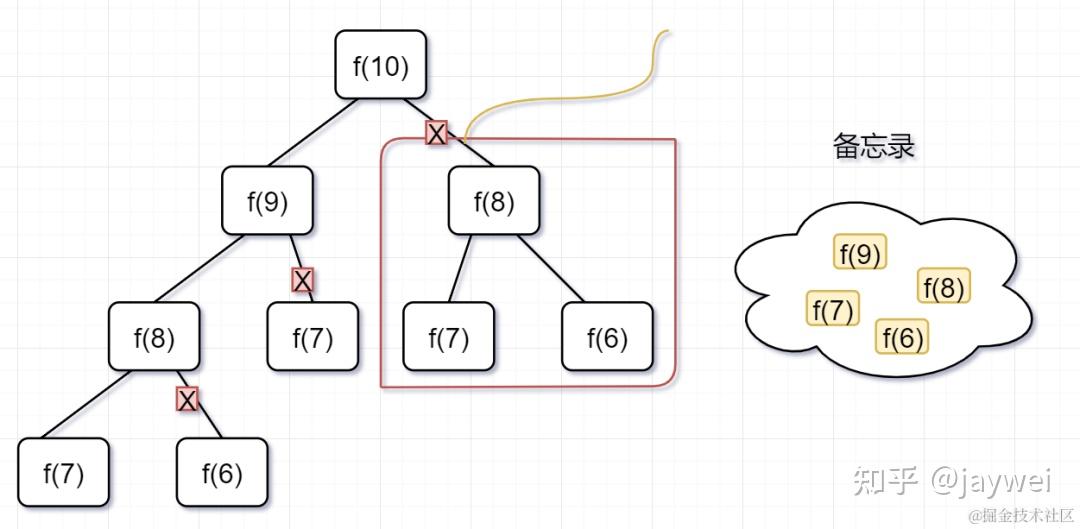
所以呢,用了备忘录递归算法,递归树变成光秃秃的树干咯,如下:
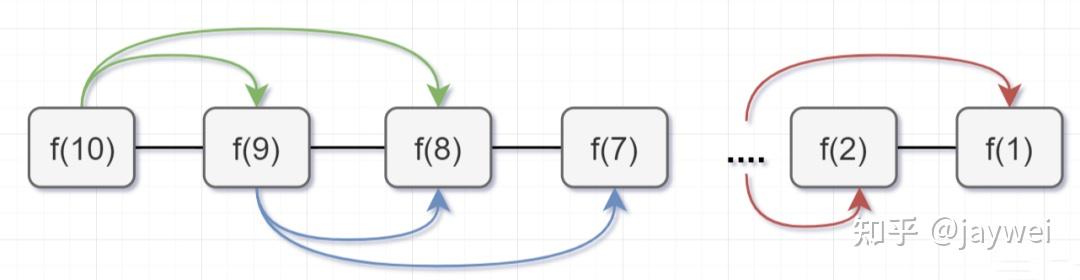
时间复杂度:带备忘录的递归算法,子问题个数=树节点数=n,解决一个子问题还是O(1),所以带备忘录的递归算法的时间复杂度是O(n)。
空间复杂度:看备忘录中,我们最终从f(10)到f(3)都记载了一遍,空间复杂度是O(n)。我们的备忘录只在最后一刻,开始求解备忘录中的子问题才得以清空——顶层问题依赖于底层问题
顶层问题依赖于底层问题,那么自底向上的求解,可以节省答案的存储空间……
保存方案二:动态规划(自底向上)
动态规划跟带备忘录的递归解法基本思想是一致的,都是减少重复计算,时间复杂度也都是差不多。但是呢:
- 带备忘录的递归,是从f(10)往f(1)方向延伸求解的,所以也称为自顶向下的解法。
- 动态规划从较小问题的解,由交叠性质,逐步决策出较大问题的解,它是从f(1)往f(10)方向,往上推求解,所以称为自底向上的解法。
我们来看下自底向上的解法,从f(1)往f(10)方向,想想是不是直接一个for循环就可以解决啦,如下:
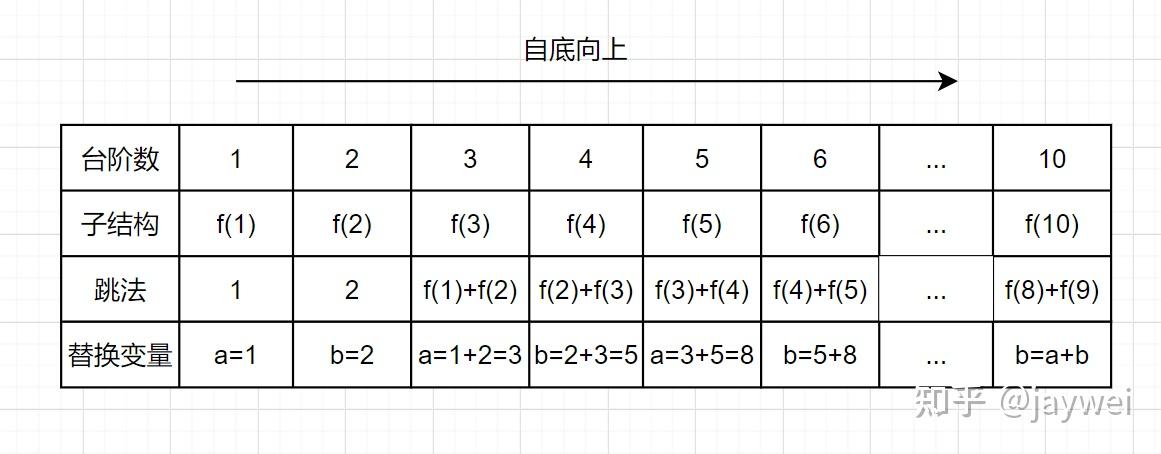
带备忘录的递归解法,空间复杂度是O(n),但是呢,仔细观察上图,可以发现,f(n) 只依赖前面两个数,所以只需要两个变量a和b来存储,就可以满足需求了,因此空间复杂度是O(1)就可以啦
其实,这就是斐波那契数列的正向生成过程。没有人会企图反向生成斐波那契数列。
动态规划有几个典型特征,最优子结构、状态转移方程、边界、重叠子问题。在青蛙跳阶问题中:
- f(n-1)和f(n-2) 足以描述 f(n) ,称为 f(n) 的最优子结构
- f(n)= f(n-1)+f(n-2) 就称为状态转移方程
- f(1) = 1, f(2) = 2 就是边界啦
- 比如f(10)= f(9)+f(8),f(9) = f(8) + f(7) ,f(8)是会重复计算的部分,就是重叠子问题
求解步骤就是
a. 找出最优解的性质,并刻划其结构特征。
b. 递归地定义最优值。
c. 以自底向上的方式计算出最优值。
d. 根据计算最优值时得到的信息,构造最优解
自底向上,一个特点就是所经过的所有信息都被输出了,这就是我们想要的规划器
Dijkstra
价值去向:路径的路程和
一文彻底搞懂Dijkstra算法(迪杰斯特拉算法) - 知乎
必须保证图中所有边(弧)的权值为非负数,否则会导致查找失败。
首先通过一个实例,给大家展示 Dijkstra 算法查找最短路径的过程。
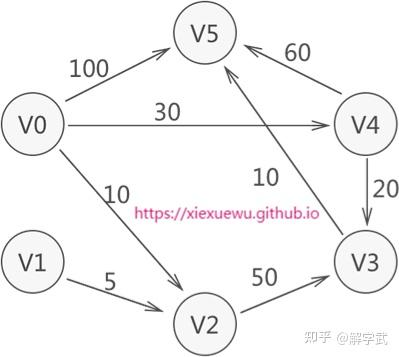
直接出发,统计从 V0 直接抵达其他路径点的路径权值
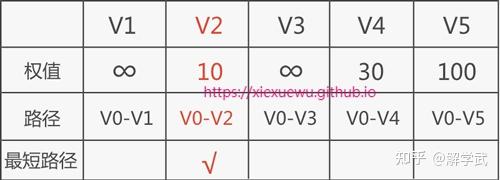
to V2 的权值成为了最小,可以断定 V0 到 V2 的最短路径就是 V0->V2,权值为10
假设存在一条比 V0->V2 权值更小的路径,比如用 V0->Vj -> ... ->V2 表示,
那么 V0->Vj 的权值一定比 V0->V2 小,表格中权值最小的路径就应该选择 V0->Vj 而不是 V0->V2。
矛盾,得证
把 V2 从目的地变更为中转站,统计从 V0 经过 V2 再到达其它顶点(排除 V2)的路径权值,一并计入表格。
| to V1 | to V3 | to V4 | to V5 | |
|---|---|---|---|---|
| V0-to | ∞ | ∞ | 30 | 100 |
| V0-V2-to | 10+∞ | 10+50 | 10+∞ | 10+∞ |
当然,表格可以上下合并(忽略下图的V2),只挑选最短的方式记录


to V4 的权值最小,所以 V0 到 V4 的最短路径就是 V0->V4,权值为30
权值最小,则任何换路都徒增权值,无需尝试换路
权值第二小,则经由权值最小之路,可能仍有更近
在已知的中转站中路径最短,则假如添加其他中转站,必定通过其他路径更长的中转站
再把 V4 从目的地变更为新中转站,统计从 V0 经过 V4 再到达其它顶点(排除 V2 V4)的路径权值,一并计入表格。
| to V1 | to V3 | to V5 | |
|---|---|---|---|
| V0-to | ∞ | ∞ | 100 |
| (V0-V2)-to | 10+∞ | 10+50 | 10+∞ |
| (V0-V4)-to | 30+∞ | 30+20 | 30+60 |
或者简并记录

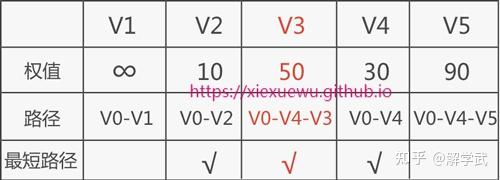
to V3 的权值最小,所以 V0 到 V3 的最短路径就是 V0->V4->V3。
再把 (V4-V3) 从目的地变更为新中转站,统计从 V0 经过【V4 和 V3】再到达其它顶点的权值,一并计入表格。
| to V1 | to V5 | |
|---|---|---|
| V0-to | ∞ | 100 |
| V0-V2-to | 10+∞ | 10+∞ |
| V0-V4-to | 30+∞ | 30+60 |
| V0-(V4-V3)-to | 50+∞ | 50+10 |
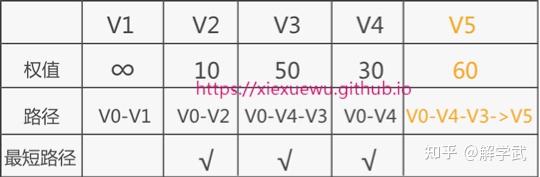
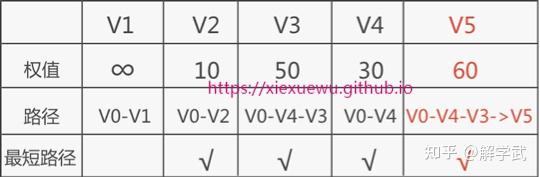
to V5 的权值最小,因此断定 V0 到 V5 的最短路径就是 V0->V4->V3->V5。
从图中可以看到,V5 顶点的出度为 0,因此无法从 V5 出发找到前往其它顶点的路径,整个算法执行结束。最终也未能找到抵达 V1 的路径,权值以无穷大表示。
查找一个顶点到其它顶点的最短路径,算法的时间复杂度为 O(n^2)。
如果需要查找网中任意两个顶点之间的最短路径,虽然对每个顶点都执行一次Dijkstra算法也可以,但更建议使用:Floyd弗洛伊德算法。
Floyd
Floyd算法详解 通俗易懂 - 知乎
弗洛伊德(Floyd)算法求图的最短路径_弗洛伊德算法求最短路径-CSDN博客
距离矩阵:多个矩阵。每个表示各个顶点之间的最短路径权值,也就是一个把图改写为正则图后的邻接矩阵。从前往后代表整个算法的历史记录。
路径矩阵:记录各个顶点之间最短走法的前驱点序号(到站前经过了谁)
- 先把距离矩阵初始化为邻接矩阵,构造正则图
- 遍历每个节点:
- 把当前点作为前驱中转站(到站前的最后一站)
- 考虑经由中转站的路程是否比直接抵达的路程更近,如果更近:
- 更新正则图的路径权值,也就是更新距离矩阵。
- 更新路径矩阵的点为新的前驱中转点
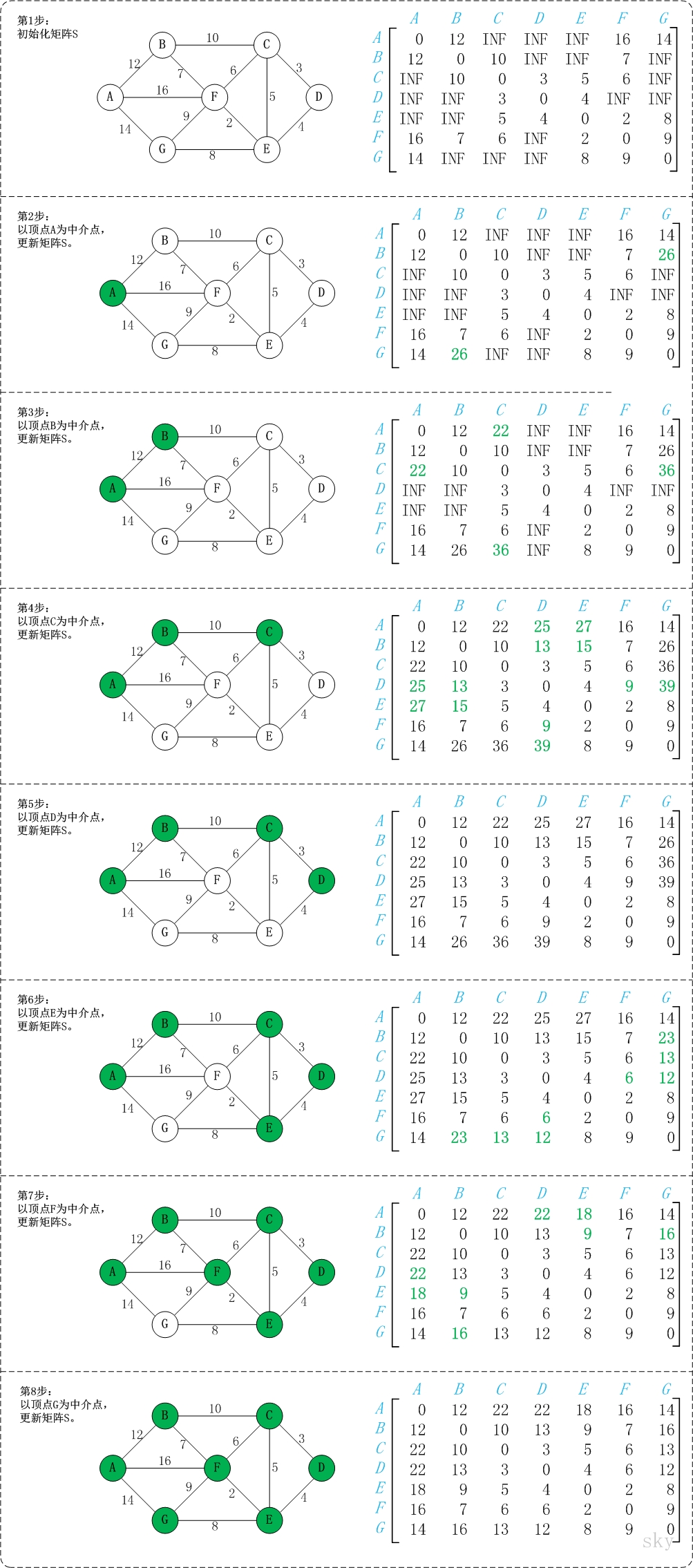
路径矩阵的覆盖更新会丢失原来的路径走法信息。如果把更新矩阵的操作变成添加副本,得到一个矩阵的阵列(“矩立方”),也就是整个算法的历史记录,就能记录任意两点最短路径的走法。
A*
A* 算法详解(个人认为最详细,最通俗易懂的一个版本)-CSDN博客
Dijkstra和A* 的区别 - 知乎
路径规划之 A* 算法 - 知乎
Dijkstra算法不使用任何关于图的全局信息,但对于机器人路径规划,我们可以轻松观测到两点的欧几里得距离,而不需要通过节点的复杂计算得出。
A* 是对Dijkstra的扩展,它通过使用启发式(heuristic)来估算从当前节点到目标节点的成本,从而加速寻路过程。
A* 算法在选择扩展哪个节点时不仅考虑到起点到当前节点的实际成本(即Dijkstra算法所做的),还考虑当前节点到终点的预估成本。
Hybird A*
【局部规划】Hybird A* 算法原理_hybrid astar-CSDN博客
动力学约束下的运动规划算法——Hybrid A* 算法(附程序实现及详细解释)pythonrobotics hybrida*-CSDN博客